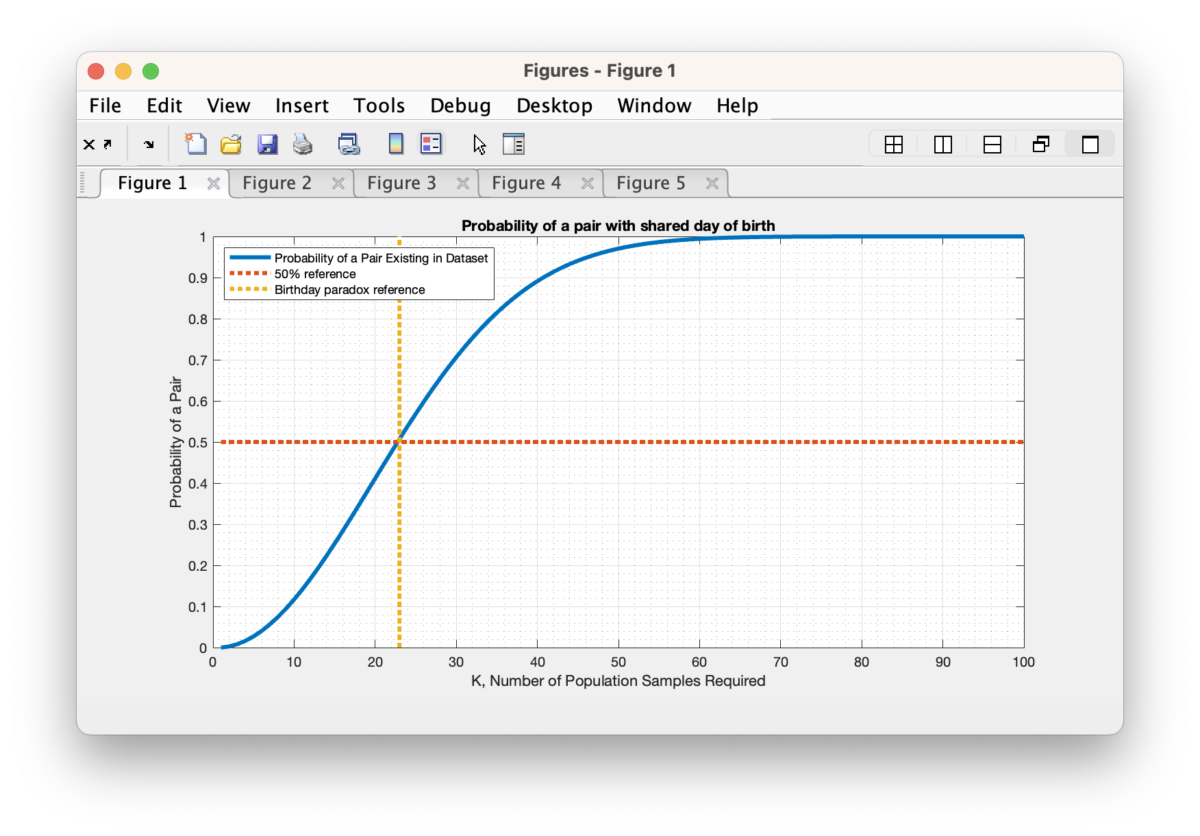
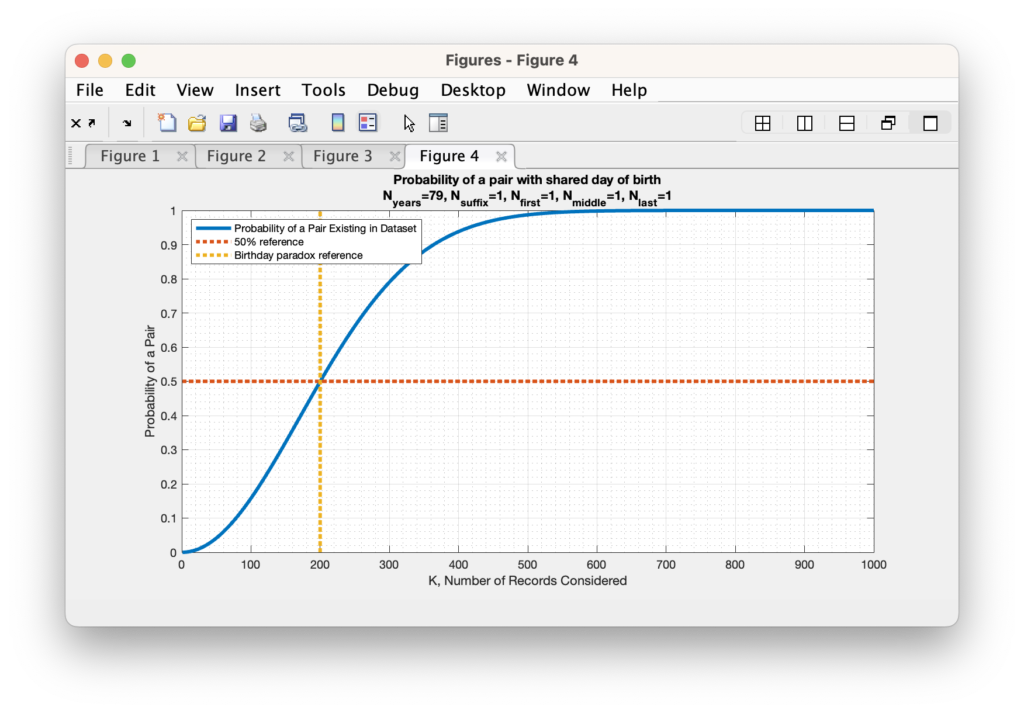
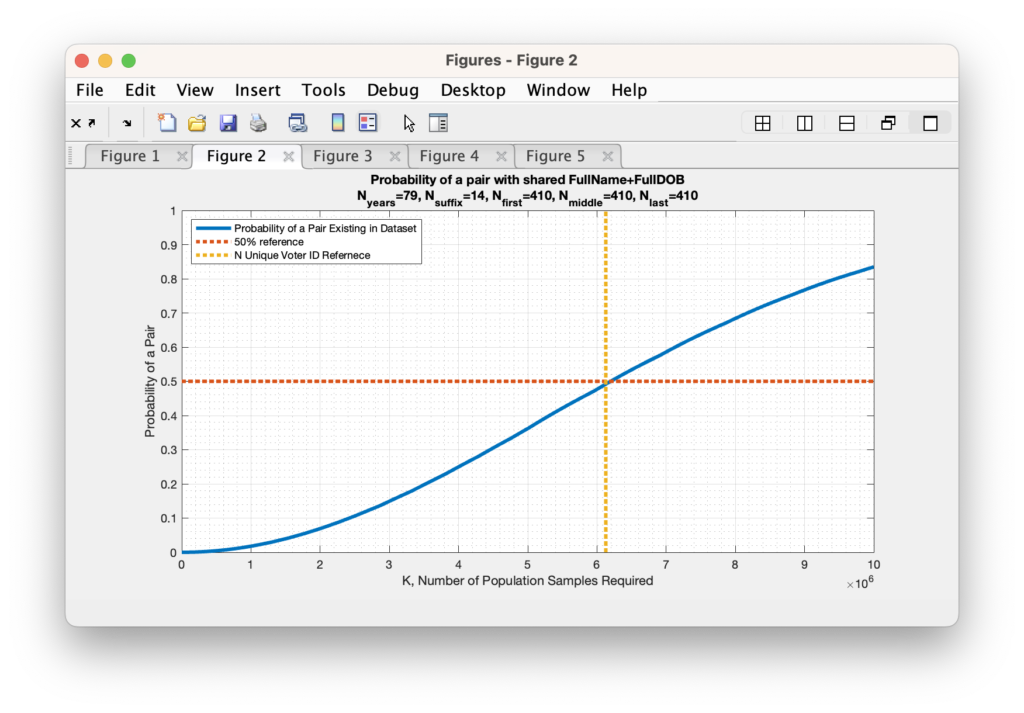
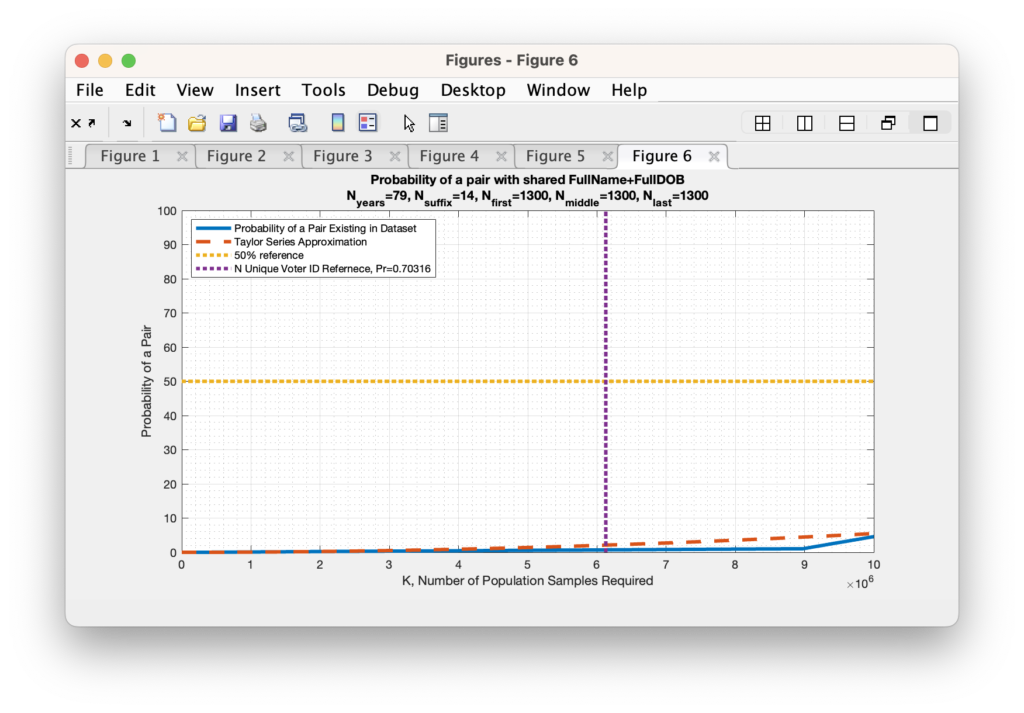
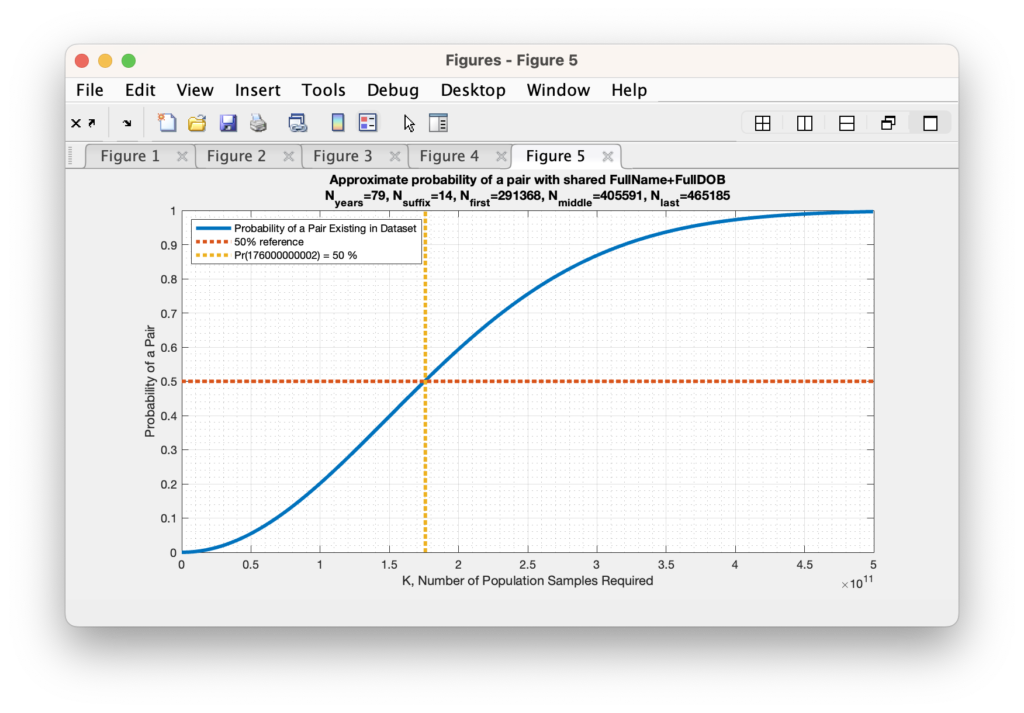
Previously I posted the computation of potential duplicate records based on string comparisons in the registered voter list. As a follow up to that article, I’ve compiled the statistics of the number of potential pairs for each locality in VA.
I tallied the number of registrant pairs with the reference match criteria defined by the MOU between ELECT and the DMV along with the two highest confidence (most stringent) match criteria that I computed. I also stratified the results by Active registrant records only or either Active or Inactive records. I also stratified by if the pairs crossed a locality boundary or not.
The table below is organized into the following computed columns, and has been sorted in decreasing order according to column 5.
- Exactly matching First + Last + DOB, which is equivalent to the MOU between ELECT and DMV.
- Exactly matching First + Middle + Last + Suffix + DOB
- Exactly matching First + Middle + Last + Suffix + DOB + Gender + Street Address
- The same as #1, but filtering for only ACTIVE voter records
- The same as #2, but filtering for only ACTIVE voter records
- The same as #3, but filtering for only ACTIVE voter records
- The same as #1, but filtering for only pairs that cross a locality boundary.
- The same as #2, but filtering for only pairs that cross a locality boundary.
- The same as #3, but filtering for only pairs that cross a locality boundary.
- The same as #4, but filtering for only pairs that cross a locality boundary.
- The same as #5, but filtering for only pairs that cross a locality boundary.
- The same as #6, but filtering for only pairs that cross a locality boundary.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| LOCALITY_NAME | Num Registrant Records | Pct Same First Last Dob | Pct Same Full Name Dob | Pct Same Full Name Dob Address | Pct Same First Last Dob _ Active Only | Pct Same Full Name Dob _ Active Only | Pct Same Full Name Dob Address _ Active Only | Pct Same First Last Dob _ xLoc | Pct Same Full Name Dob _ xLoc | Pct Same Full Name Dob Address _ xLoc | Pct Same First Last Dob _ Active Only _ xLoc | Pct Same Full Name Dob _ Active Only _ xLoc | Pct Same Full Name Dob Address _ Active Only _ xLoc |
| NORTON CITY | 2604 | 0.2304% | 0.2304% | 0.1536% | 0.1920% | 0.1920% | 0.1536% | 0.0768% | 0.0768% | 0.0000% | 0.0384% | 0.0384% | 0.0000% |
| NOTTOWAY COUNTY | 9704 | 0.2988% | 0.2061% | 0.0618% | 0.2473% | 0.1752% | 0.0618% | 0.2370% | 0.1649% | 0.0206% | 0.1855% | 0.1340% | 0.0206% |
| RADFORD CITY | 9551 | 0.4293% | 0.2827% | 0.0000% | 0.2827% | 0.1675% | 0.0000% | 0.4293% | 0.2827% | 0.0000% | 0.2827% | 0.1675% | 0.0000% |
| HIGHLAND COUNTY | 1903 | 0.2627% | 0.1576% | 0.1051% | 0.2627% | 0.1576% | 0.1051% | 0.1576% | 0.0525% | 0.0000% | 0.1576% | 0.0525% | 0.0000% |
| WILLIAMSBURG CITY | 10480 | 0.2195% | 0.1336% | 0.0000% | 0.2004% | 0.1336% | 0.0000% | 0.2004% | 0.1336% | 0.0000% | 0.1813% | 0.1336% | 0.0000% |
| LYNCHBURG CITY | 56319 | 0.3072% | 0.1829% | 0.0533% | 0.2255% | 0.1296% | 0.0533% | 0.1616% | 0.0764% | 0.0000% | 0.1190% | 0.0479% | 0.0000% |
| EMPORIA CITY | 4023 | 0.3480% | 0.1740% | 0.0000% | 0.2983% | 0.1243% | 0.0000% | 0.2486% | 0.0746% | 0.0000% | 0.1989% | 0.0249% | 0.0000% |
| SUFFOLK CITY | 71580 | 0.2403% | 0.1229% | 0.0754% | 0.2249% | 0.1187% | 0.0754% | 0.1229% | 0.0307% | 0.0000% | 0.1104% | 0.0265% | 0.0000% |
| FALLS CHURCH CITY | 11213 | 0.1784% | 0.1338% | 0.0357% | 0.1516% | 0.1159% | 0.0178% | 0.0892% | 0.0624% | 0.0000% | 0.0803% | 0.0624% | 0.0000% |
| SUSSEX COUNTY | 7149 | 0.2658% | 0.1259% | 0.0839% | 0.2238% | 0.1119% | 0.0839% | 0.1539% | 0.0140% | 0.0000% | 0.1119% | 0.0000% | 0.0000% |
| FRANKLIN CITY | 5924 | 0.2026% | 0.1182% | 0.0338% | 0.1857% | 0.1013% | 0.0338% | 0.1688% | 0.0844% | 0.0000% | 0.1519% | 0.0675% | 0.0000% |
| APPOMATTOX COUNTY | 12195 | 0.2542% | 0.1230% | 0.0328% | 0.2214% | 0.0902% | 0.0328% | 0.2050% | 0.0738% | 0.0000% | 0.1886% | 0.0574% | 0.0000% |
| LEE COUNTY | 15619 | 0.2497% | 0.0960% | 0.0128% | 0.2305% | 0.0832% | 0.0128% | 0.1473% | 0.0192% | 0.0000% | 0.1409% | 0.0192% | 0.0000% |
| ALBEMARLE COUNTY | 84889 | 0.1920% | 0.1001% | 0.0212% | 0.1590% | 0.0825% | 0.0188% | 0.1402% | 0.0554% | 0.0000% | 0.1096% | 0.0401% | 0.0000% |
| AMHERST COUNTY | 22906 | 0.1965% | 0.0829% | 0.0437% | 0.1790% | 0.0742% | 0.0437% | 0.1441% | 0.0393% | 0.0000% | 0.1266% | 0.0306% | 0.0000% |
| PRINCE EDWARD COUNTY | 13595 | 0.2280% | 0.0883% | 0.0000% | 0.1912% | 0.0662% | 0.0000% | 0.2133% | 0.0883% | 0.0000% | 0.1765% | 0.0662% | 0.0000% |
| STAUNTON CITY | 18180 | 0.1980% | 0.0935% | 0.0000% | 0.1595% | 0.0605% | 0.0000% | 0.1650% | 0.0605% | 0.0000% | 0.1265% | 0.0275% | 0.0000% |
| NELSON COUNTY | 11895 | 0.1765% | 0.0673% | 0.0168% | 0.1513% | 0.0588% | 0.0168% | 0.1261% | 0.0504% | 0.0000% | 0.1177% | 0.0420% | 0.0000% |
| ARLINGTON COUNTY | 177092 | 0.1378% | 0.0683% | 0.0113% | 0.1146% | 0.0576% | 0.0102% | 0.0870% | 0.0344% | 0.0000% | 0.0683% | 0.0260% | 0.0000% |
| NORTHUMBERLAND COUNTY | 10457 | 0.1339% | 0.0574% | 0.0191% | 0.1243% | 0.0574% | 0.0191% | 0.0956% | 0.0191% | 0.0000% | 0.0861% | 0.0191% | 0.0000% |
| SOUTHAMPTON COUNTY | 13218 | 0.2194% | 0.0757% | 0.0000% | 0.1740% | 0.0530% | 0.0000% | 0.1589% | 0.0454% | 0.0000% | 0.1286% | 0.0227% | 0.0000% |
| HOPEWELL CITY | 15825 | 0.2401% | 0.0695% | 0.0253% | 0.2085% | 0.0506% | 0.0253% | 0.1390% | 0.0190% | 0.0000% | 0.1201% | 0.0126% | 0.0000% |
| LUNENBURG COUNTY | 8097 | 0.1853% | 0.0618% | 0.0000% | 0.1729% | 0.0494% | 0.0000% | 0.1853% | 0.0618% | 0.0000% | 0.1729% | 0.0494% | 0.0000% |
| AMELIA COUNTY | 10179 | 0.1375% | 0.0884% | 0.0098% | 0.0884% | 0.0491% | 0.0098% | 0.1375% | 0.0884% | 0.0098% | 0.0884% | 0.0491% | 0.0098% |
| RICHMOND CITY | 161097 | 0.1707% | 0.0639% | 0.0000% | 0.1316% | 0.0490% | 0.0000% | 0.1459% | 0.0528% | 0.0000% | 0.1155% | 0.0416% | 0.0000% |
| CHARLOTTESVILLE CITY | 34789 | 0.1265% | 0.0604% | 0.0000% | 0.1064% | 0.0489% | 0.0000% | 0.1150% | 0.0489% | 0.0000% | 0.0949% | 0.0374% | 0.0000% |
| LEXINGTON CITY | 4211 | 0.2612% | 0.1187% | 0.0000% | 0.1900% | 0.0475% | 0.0000% | 0.2612% | 0.1187% | 0.0000% | 0.1900% | 0.0475% | 0.0000% |
| FAIRFAX COUNTY | 787727 | 0.1143% | 0.0559% | 0.0053% | 0.0988% | 0.0474% | 0.0053% | 0.0665% | 0.0236% | 0.0000% | 0.0546% | 0.0171% | 0.0000% |
| CHARLOTTE COUNTY | 8474 | 0.2242% | 0.0708% | 0.0236% | 0.1652% | 0.0472% | 0.0236% | 0.2006% | 0.0472% | 0.0000% | 0.1416% | 0.0236% | 0.0000% |
| HARRISONBURG CITY | 26443 | 0.1777% | 0.0870% | 0.0000% | 0.1210% | 0.0454% | 0.0000% | 0.1324% | 0.0567% | 0.0000% | 0.0908% | 0.0303% | 0.0000% |
| BRUNSWICK COUNTY | 11098 | 0.2253% | 0.0631% | 0.0000% | 0.1982% | 0.0451% | 0.0000% | 0.2072% | 0.0451% | 0.0000% | 0.1802% | 0.0270% | 0.0000% |
| HAMPTON CITY | 100807 | 0.2044% | 0.0764% | 0.0060% | 0.1468% | 0.0446% | 0.0040% | 0.1210% | 0.0387% | 0.0000% | 0.0972% | 0.0268% | 0.0000% |
| WISE COUNTY | 24750 | 0.1455% | 0.0525% | 0.0000% | 0.1333% | 0.0444% | 0.0000% | 0.1212% | 0.0364% | 0.0000% | 0.1091% | 0.0283% | 0.0000% |
| WYTHE COUNTY | 20950 | 0.1480% | 0.0525% | 0.0191% | 0.1289% | 0.0430% | 0.0191% | 0.1002% | 0.0143% | 0.0000% | 0.0907% | 0.0143% | 0.0000% |
| CHESAPEAKE CITY | 178005 | 0.1258% | 0.0433% | 0.0303% | 0.1140% | 0.0410% | 0.0303% | 0.0843% | 0.0062% | 0.0000% | 0.0747% | 0.0051% | 0.0000% |
| NEWPORT NEWS CITY | 124778 | 0.1354% | 0.0537% | 0.0016% | 0.1122% | 0.0409% | 0.0016% | 0.1002% | 0.0313% | 0.0000% | 0.0850% | 0.0216% | 0.0000% |
| CUMBERLAND COUNTY | 7416 | 0.1483% | 0.0539% | 0.0270% | 0.1214% | 0.0405% | 0.0270% | 0.1214% | 0.0270% | 0.0000% | 0.0944% | 0.0135% | 0.0000% |
| PRINCE GEORGE COUNTY | 24957 | 0.1643% | 0.0401% | 0.0000% | 0.1322% | 0.0401% | 0.0000% | 0.1643% | 0.0401% | 0.0000% | 0.1322% | 0.0401% | 0.0000% |
| HALIFAX COUNTY | 25086 | 0.1196% | 0.0438% | 0.0239% | 0.1156% | 0.0399% | 0.0239% | 0.0877% | 0.0120% | 0.0000% | 0.0837% | 0.0080% | 0.0000% |
| SMYTH COUNTY | 20159 | 0.1339% | 0.0397% | 0.0000% | 0.1290% | 0.0397% | 0.0000% | 0.1141% | 0.0198% | 0.0000% | 0.1091% | 0.0198% | 0.0000% |
| FAIRFAX CITY | 17825 | 0.1234% | 0.0617% | 0.0000% | 0.0954% | 0.0393% | 0.0000% | 0.1122% | 0.0617% | 0.0000% | 0.0842% | 0.0393% | 0.0000% |
| CAMPBELL COUNTY | 41318 | 0.1380% | 0.0508% | 0.0048% | 0.1186% | 0.0387% | 0.0048% | 0.1283% | 0.0411% | 0.0000% | 0.1089% | 0.0290% | 0.0000% |
| COLONIAL HEIGHTS CITY | 13066 | 0.0918% | 0.0383% | 0.0000% | 0.0918% | 0.0383% | 0.0000% | 0.0918% | 0.0383% | 0.0000% | 0.0918% | 0.0383% | 0.0000% |
| CHESTERFIELD COUNTY | 270084 | 0.1529% | 0.0478% | 0.0067% | 0.1300% | 0.0381% | 0.0059% | 0.1107% | 0.0248% | 0.0000% | 0.0937% | 0.0196% | 0.0000% |
| PETERSBURG CITY | 23740 | 0.1685% | 0.0421% | 0.0000% | 0.1559% | 0.0379% | 0.0000% | 0.1601% | 0.0421% | 0.0000% | 0.1474% | 0.0379% | 0.0000% |
| SURRY COUNTY | 5675 | 0.1762% | 0.0352% | 0.0000% | 0.1410% | 0.0352% | 0.0000% | 0.1410% | 0.0000% | 0.0000% | 0.1057% | 0.0000% | 0.0000% |
| STAFFORD COUNTY | 111261 | 0.1222% | 0.0440% | 0.0072% | 0.1079% | 0.0351% | 0.0072% | 0.1007% | 0.0279% | 0.0000% | 0.0881% | 0.0207% | 0.0000% |
| BUCHANAN COUNTY | 14836 | 0.0876% | 0.0337% | 0.0000% | 0.0876% | 0.0337% | 0.0000% | 0.0607% | 0.0067% | 0.0000% | 0.0607% | 0.0067% | 0.0000% |
| PORTSMOUTH CITY | 68381 | 0.1536% | 0.0409% | 0.0058% | 0.1375% | 0.0336% | 0.0058% | 0.1185% | 0.0263% | 0.0000% | 0.1024% | 0.0190% | 0.0000% |
| PITTSYLVANIA COUNTY | 45322 | 0.1677% | 0.0441% | 0.0044% | 0.1522% | 0.0331% | 0.0044% | 0.1324% | 0.0221% | 0.0000% | 0.1214% | 0.0154% | 0.0000% |
| MECKLENBURG COUNTY | 22996 | 0.1522% | 0.0478% | 0.0000% | 0.1305% | 0.0304% | 0.0000% | 0.1261% | 0.0391% | 0.0000% | 0.1131% | 0.0304% | 0.0000% |
| NORTHAMPTON COUNTY | 9877 | 0.0911% | 0.0304% | 0.0202% | 0.0810% | 0.0304% | 0.0202% | 0.0911% | 0.0101% | 0.0000% | 0.0810% | 0.0101% | 0.0000% |
| PAGE COUNTY | 17095 | 0.1872% | 0.0351% | 0.0000% | 0.1521% | 0.0292% | 0.0000% | 0.1521% | 0.0117% | 0.0000% | 0.1170% | 0.0058% | 0.0000% |
| ACCOMACK COUNTY | 25483 | 0.1216% | 0.0275% | 0.0000% | 0.1020% | 0.0275% | 0.0000% | 0.1138% | 0.0275% | 0.0000% | 0.0942% | 0.0275% | 0.0000% |
| GRAYSON COUNTY | 10941 | 0.1645% | 0.0274% | 0.0000% | 0.1554% | 0.0274% | 0.0000% | 0.1462% | 0.0274% | 0.0000% | 0.1371% | 0.0274% | 0.0000% |
| ALLEGHANY COUNTY | 11069 | 0.1355% | 0.0271% | 0.0000% | 0.1084% | 0.0271% | 0.0000% | 0.0994% | 0.0090% | 0.0000% | 0.0723% | 0.0090% | 0.0000% |
| MATHEWS COUNTY | 7378 | 0.0949% | 0.0271% | 0.0271% | 0.0678% | 0.0271% | 0.0271% | 0.0678% | 0.0000% | 0.0000% | 0.0407% | 0.0000% | 0.0000% |
| BEDFORD COUNTY | 63240 | 0.1233% | 0.0300% | 0.0063% | 0.1154% | 0.0269% | 0.0063% | 0.1012% | 0.0142% | 0.0000% | 0.0933% | 0.0111% | 0.0000% |
| HENRICO COUNTY | 240436 | 0.1152% | 0.0299% | 0.0083% | 0.0998% | 0.0258% | 0.0083% | 0.0944% | 0.0175% | 0.0000% | 0.0807% | 0.0133% | 0.0000% |
| WAYNESBORO CITY | 15561 | 0.1735% | 0.0450% | 0.0000% | 0.1285% | 0.0257% | 0.0000% | 0.1735% | 0.0450% | 0.0000% | 0.1285% | 0.0257% | 0.0000% |
| HANOVER COUNTY | 87000 | 0.1092% | 0.0287% | 0.0023% | 0.1011% | 0.0253% | 0.0023% | 0.1023% | 0.0218% | 0.0000% | 0.0943% | 0.0184% | 0.0000% |
| CRAIG COUNTY | 3972 | 0.1007% | 0.0252% | 0.0000% | 0.1007% | 0.0252% | 0.0000% | 0.1007% | 0.0252% | 0.0000% | 0.1007% | 0.0252% | 0.0000% |
| GALAX CITY | 4067 | 0.1229% | 0.0246% | 0.0000% | 0.1229% | 0.0246% | 0.0000% | 0.1229% | 0.0246% | 0.0000% | 0.1229% | 0.0246% | 0.0000% |
| ORANGE COUNTY | 28482 | 0.1299% | 0.0351% | 0.0000% | 0.1194% | 0.0246% | 0.0000% | 0.1299% | 0.0351% | 0.0000% | 0.1194% | 0.0246% | 0.0000% |
| DANVILLE CITY | 28838 | 0.1040% | 0.0312% | 0.0000% | 0.0902% | 0.0243% | 0.0000% | 0.1040% | 0.0312% | 0.0000% | 0.0902% | 0.0243% | 0.0000% |
| CARROLL COUNTY | 21163 | 0.1040% | 0.0236% | 0.0095% | 0.1040% | 0.0236% | 0.0095% | 0.0945% | 0.0142% | 0.0000% | 0.0945% | 0.0142% | 0.0000% |
| FREDERICK COUNTY | 67912 | 0.1075% | 0.0324% | 0.0088% | 0.0883% | 0.0236% | 0.0059% | 0.0898% | 0.0206% | 0.0000% | 0.0736% | 0.0147% | 0.0000% |
| MANASSAS PARK CITY | 9018 | 0.0665% | 0.0222% | 0.0000% | 0.0554% | 0.0222% | 0.0000% | 0.0444% | 0.0222% | 0.0000% | 0.0333% | 0.0222% | 0.0000% |
| HENRY COUNTY | 36539 | 0.1259% | 0.0246% | 0.0000% | 0.1122% | 0.0219% | 0.0000% | 0.0931% | 0.0082% | 0.0000% | 0.0848% | 0.0055% | 0.0000% |
| BLAND COUNTY | 4581 | 0.1091% | 0.0218% | 0.0000% | 0.1091% | 0.0218% | 0.0000% | 0.1091% | 0.0218% | 0.0000% | 0.1091% | 0.0218% | 0.0000% |
| SPOTSYLVANIA COUNTY | 105361 | 0.0987% | 0.0247% | 0.0057% | 0.0873% | 0.0218% | 0.0057% | 0.0816% | 0.0095% | 0.0000% | 0.0702% | 0.0066% | 0.0000% |
| WINCHESTER CITY | 18352 | 0.1035% | 0.0381% | 0.0000% | 0.0708% | 0.0218% | 0.0000% | 0.0926% | 0.0381% | 0.0000% | 0.0599% | 0.0218% | 0.0000% |
| LANCASTER COUNTY | 9267 | 0.0755% | 0.0216% | 0.0000% | 0.0755% | 0.0216% | 0.0000% | 0.0755% | 0.0216% | 0.0000% | 0.0755% | 0.0216% | 0.0000% |
| KING WILLIAM COUNTY | 13996 | 0.1286% | 0.0214% | 0.0000% | 0.1143% | 0.0214% | 0.0000% | 0.1286% | 0.0214% | 0.0000% | 0.1143% | 0.0214% | 0.0000% |
| WESTMORELAND COUNTY | 14233 | 0.1827% | 0.0211% | 0.0000% | 0.1756% | 0.0211% | 0.0000% | 0.1546% | 0.0211% | 0.0000% | 0.1475% | 0.0211% | 0.0000% |
| VIRGINIA BEACH CITY | 331914 | 0.1118% | 0.0259% | 0.0066% | 0.0967% | 0.0208% | 0.0066% | 0.0883% | 0.0114% | 0.0000% | 0.0762% | 0.0081% | 0.0000% |
| POWHATAN COUNTY | 24287 | 0.1400% | 0.0371% | 0.0000% | 0.1153% | 0.0206% | 0.0000% | 0.1400% | 0.0371% | 0.0000% | 0.1153% | 0.0206% | 0.0000% |
| BOTETOURT COUNTY | 26311 | 0.1178% | 0.0190% | 0.0076% | 0.1102% | 0.0190% | 0.0076% | 0.1102% | 0.0114% | 0.0000% | 0.1026% | 0.0114% | 0.0000% |
| FLUVANNA COUNTY | 21001 | 0.1286% | 0.0238% | 0.0000% | 0.1190% | 0.0190% | 0.0000% | 0.1095% | 0.0238% | 0.0000% | 0.1000% | 0.0190% | 0.0000% |
| SCOTT COUNTY | 16059 | 0.1121% | 0.0249% | 0.0000% | 0.1059% | 0.0187% | 0.0000% | 0.0996% | 0.0125% | 0.0000% | 0.0934% | 0.0062% | 0.0000% |
| ALEXANDRIA CITY | 112212 | 0.0820% | 0.0205% | 0.0000% | 0.0686% | 0.0178% | 0.0000% | 0.0784% | 0.0169% | 0.0000% | 0.0651% | 0.0143% | 0.0000% |
| TAZEWELL COUNTY | 28147 | 0.0995% | 0.0178% | 0.0142% | 0.0959% | 0.0178% | 0.0142% | 0.0853% | 0.0036% | 0.0000% | 0.0817% | 0.0036% | 0.0000% |
| RICHMOND COUNTY | 5649 | 0.2301% | 0.0354% | 0.0000% | 0.1947% | 0.0177% | 0.0000% | 0.1947% | 0.0354% | 0.0000% | 0.1593% | 0.0177% | 0.0000% |
| ROCKINGHAM COUNTY | 56817 | 0.0845% | 0.0246% | 0.0035% | 0.0739% | 0.0176% | 0.0000% | 0.0739% | 0.0176% | 0.0000% | 0.0669% | 0.0141% | 0.0000% |
| LOUISA COUNTY | 29567 | 0.1150% | 0.0271% | 0.0135% | 0.1015% | 0.0169% | 0.0135% | 0.1082% | 0.0135% | 0.0000% | 0.0947% | 0.0034% | 0.0000% |
| LOUDOUN COUNTY | 291914 | 0.0740% | 0.0219% | 0.0041% | 0.0620% | 0.0164% | 0.0041% | 0.0651% | 0.0171% | 0.0000% | 0.0531% | 0.0116% | 0.0000% |
| RAPPAHANNOCK COUNTY | 6239 | 0.0962% | 0.0160% | 0.0000% | 0.0801% | 0.0160% | 0.0000% | 0.0962% | 0.0160% | 0.0000% | 0.0801% | 0.0160% | 0.0000% |
| JAMES CITY COUNTY | 64390 | 0.0745% | 0.0186% | 0.0000% | 0.0668% | 0.0155% | 0.0000% | 0.0621% | 0.0124% | 0.0000% | 0.0544% | 0.0093% | 0.0000% |
| PATRICK COUNTY | 12862 | 0.0855% | 0.0155% | 0.0000% | 0.0777% | 0.0155% | 0.0000% | 0.0855% | 0.0155% | 0.0000% | 0.0777% | 0.0155% | 0.0000% |
| PRINCE WILLIAM COUNTY | 316530 | 0.0812% | 0.0186% | 0.0000% | 0.0663% | 0.0148% | 0.0000% | 0.0711% | 0.0142% | 0.0000% | 0.0581% | 0.0104% | 0.0000% |
| AUGUSTA COUNTY | 54993 | 0.1455% | 0.0218% | 0.0036% | 0.1255% | 0.0145% | 0.0036% | 0.1346% | 0.0182% | 0.0000% | 0.1146% | 0.0109% | 0.0000% |
| DINWIDDIE COUNTY | 20835 | 0.1584% | 0.0384% | 0.0048% | 0.1152% | 0.0144% | 0.0048% | 0.1488% | 0.0288% | 0.0048% | 0.1152% | 0.0144% | 0.0048% |
| GOOCHLAND COUNTY | 21410 | 0.1261% | 0.0187% | 0.0000% | 0.1121% | 0.0140% | 0.0000% | 0.1261% | 0.0187% | 0.0000% | 0.1121% | 0.0140% | 0.0000% |
| MONTGOMERY COUNTY | 61944 | 0.0936% | 0.0145% | 0.0000% | 0.0807% | 0.0129% | 0.0000% | 0.0904% | 0.0145% | 0.0000% | 0.0775% | 0.0129% | 0.0000% |
| SHENANDOAH COUNTY | 32304 | 0.0960% | 0.0155% | 0.0000% | 0.0743% | 0.0124% | 0.0000% | 0.0960% | 0.0155% | 0.0000% | 0.0743% | 0.0124% | 0.0000% |
| ROANOKE COUNTY | 73467 | 0.0953% | 0.0163% | 0.0027% | 0.0830% | 0.0123% | 0.0027% | 0.0817% | 0.0109% | 0.0000% | 0.0694% | 0.0068% | 0.0000% |
| SALEM CITY | 17932 | 0.0892% | 0.0112% | 0.0000% | 0.0781% | 0.0112% | 0.0000% | 0.0892% | 0.0112% | 0.0000% | 0.0781% | 0.0112% | 0.0000% |
| NEW KENT COUNTY | 19022 | 0.1051% | 0.0210% | 0.0000% | 0.0894% | 0.0105% | 0.0000% | 0.0946% | 0.0210% | 0.0000% | 0.0789% | 0.0105% | 0.0000% |
| WASHINGTON COUNTY | 39449 | 0.1014% | 0.0152% | 0.0000% | 0.0887% | 0.0101% | 0.0000% | 0.0862% | 0.0051% | 0.0000% | 0.0786% | 0.0051% | 0.0000% |
| MADISON COUNTY | 10407 | 0.0865% | 0.0192% | 0.0000% | 0.0769% | 0.0096% | 0.0000% | 0.0865% | 0.0192% | 0.0000% | 0.0769% | 0.0096% | 0.0000% |
| NORFOLK CITY | 141236 | 0.0984% | 0.0092% | 0.0000% | 0.0864% | 0.0085% | 0.0000% | 0.0899% | 0.0064% | 0.0000% | 0.0793% | 0.0057% | 0.0000% |
| PULASKI COUNTY | 23825 | 0.0881% | 0.0126% | 0.0000% | 0.0756% | 0.0084% | 0.0000% | 0.0881% | 0.0126% | 0.0000% | 0.0756% | 0.0084% | 0.0000% |
| CLARKE COUNTY | 12269 | 0.1060% | 0.0163% | 0.0000% | 0.0978% | 0.0082% | 0.0000% | 0.1060% | 0.0163% | 0.0000% | 0.0978% | 0.0082% | 0.0000% |
| GREENE COUNTY | 14926 | 0.1072% | 0.0067% | 0.0000% | 0.1072% | 0.0067% | 0.0000% | 0.1072% | 0.0067% | 0.0000% | 0.1072% | 0.0067% | 0.0000% |
| GLOUCESTER COUNTY | 30284 | 0.0859% | 0.0066% | 0.0000% | 0.0859% | 0.0066% | 0.0000% | 0.0859% | 0.0066% | 0.0000% | 0.0859% | 0.0066% | 0.0000% |
| WARREN COUNTY | 30517 | 0.0885% | 0.0066% | 0.0000% | 0.0852% | 0.0066% | 0.0000% | 0.0819% | 0.0066% | 0.0000% | 0.0786% | 0.0066% | 0.0000% |
| ISLE OF WIGHT COUNTY | 31179 | 0.0898% | 0.0064% | 0.0000% | 0.0834% | 0.0064% | 0.0000% | 0.0898% | 0.0064% | 0.0000% | 0.0834% | 0.0064% | 0.0000% |
| ROCKBRIDGE COUNTY | 16266 | 0.1230% | 0.0123% | 0.0000% | 0.1045% | 0.0061% | 0.0000% | 0.1230% | 0.0123% | 0.0000% | 0.1045% | 0.0061% | 0.0000% |
| CULPEPER COUNTY | 37117 | 0.0943% | 0.0108% | 0.0000% | 0.0808% | 0.0054% | 0.0000% | 0.0889% | 0.0108% | 0.0000% | 0.0754% | 0.0054% | 0.0000% |
| FAUQUIER COUNTY | 56396 | 0.0887% | 0.0071% | 0.0000% | 0.0762% | 0.0053% | 0.0000% | 0.0887% | 0.0071% | 0.0000% | 0.0762% | 0.0053% | 0.0000% |
| FREDERICKSBURG CITY | 19455 | 0.0874% | 0.0051% | 0.0000% | 0.0720% | 0.0051% | 0.0000% | 0.0874% | 0.0051% | 0.0000% | 0.0720% | 0.0051% | 0.0000% |
| FRANKLIN COUNTY | 39866 | 0.0602% | 0.0050% | 0.0050% | 0.0502% | 0.0050% | 0.0050% | 0.0552% | 0.0000% | 0.0000% | 0.0452% | 0.0000% | 0.0000% |
| MANASSAS CITY | 23815 | 0.1008% | 0.0042% | 0.0000% | 0.0966% | 0.0042% | 0.0000% | 0.0840% | 0.0042% | 0.0000% | 0.0798% | 0.0042% | 0.0000% |
| YORK COUNTY | 50838 | 0.0925% | 0.0157% | 0.0000% | 0.0669% | 0.0039% | 0.0000% | 0.0885% | 0.0157% | 0.0000% | 0.0629% | 0.0039% | 0.0000% |
| BATH COUNTY | 3358 | 0.0893% | 0.0000% | 0.0000% | 0.0893% | 0.0000% | 0.0000% | 0.0893% | 0.0000% | 0.0000% | 0.0893% | 0.0000% | 0.0000% |
| BRISTOL CITY | 12345 | 0.0729% | 0.0000% | 0.0000% | 0.0567% | 0.0000% | 0.0000% | 0.0567% | 0.0000% | 0.0000% | 0.0567% | 0.0000% | 0.0000% |
| BUCKINGHAM COUNTY | 11063 | 0.1356% | 0.0271% | 0.0000% | 0.0904% | 0.0000% | 0.0000% | 0.1356% | 0.0271% | 0.0000% | 0.0904% | 0.0000% | 0.0000% |
| BUENA VISTA CITY | 4432 | 0.0903% | 0.0000% | 0.0000% | 0.0903% | 0.0000% | 0.0000% | 0.0903% | 0.0000% | 0.0000% | 0.0903% | 0.0000% | 0.0000% |
| CAROLINE COUNTY | 22894 | 0.1005% | 0.0087% | 0.0000% | 0.0830% | 0.0000% | 0.0000% | 0.1005% | 0.0087% | 0.0000% | 0.0830% | 0.0000% | 0.0000% |
| CHARLES CITY COUNTY | 5720 | 0.0524% | 0.0000% | 0.0000% | 0.0350% | 0.0000% | 0.0000% | 0.0524% | 0.0000% | 0.0000% | 0.0350% | 0.0000% | 0.0000% |
| COVINGTON CITY | 3888 | 0.1029% | 0.0000% | 0.0000% | 0.0772% | 0.0000% | 0.0000% | 0.1029% | 0.0000% | 0.0000% | 0.0772% | 0.0000% | 0.0000% |
| DICKENSON COUNTY | 10144 | 0.1084% | 0.0000% | 0.0000% | 0.0887% | 0.0000% | 0.0000% | 0.1084% | 0.0000% | 0.0000% | 0.0887% | 0.0000% | 0.0000% |
| ESSEX COUNTY | 8318 | 0.1443% | 0.0000% | 0.0000% | 0.1443% | 0.0000% | 0.0000% | 0.1443% | 0.0000% | 0.0000% | 0.1443% | 0.0000% | 0.0000% |
| FLOYD COUNTY | 11852 | 0.0759% | 0.0000% | 0.0000% | 0.0759% | 0.0000% | 0.0000% | 0.0759% | 0.0000% | 0.0000% | 0.0759% | 0.0000% | 0.0000% |
| GILES COUNTY | 12093 | 0.0413% | 0.0000% | 0.0000% | 0.0331% | 0.0000% | 0.0000% | 0.0413% | 0.0000% | 0.0000% | 0.0331% | 0.0000% | 0.0000% |
| GREENSVILLE COUNTY | 6435 | 0.1709% | 0.0155% | 0.0000% | 0.1399% | 0.0000% | 0.0000% | 0.1709% | 0.0155% | 0.0000% | 0.1399% | 0.0000% | 0.0000% |
| KING AND QUEEN COUNTY | 5403 | 0.0740% | 0.0000% | 0.0000% | 0.0740% | 0.0000% | 0.0000% | 0.0740% | 0.0000% | 0.0000% | 0.0740% | 0.0000% | 0.0000% |
| KING GEORGE COUNTY | 19780 | 0.1314% | 0.0000% | 0.0000% | 0.0910% | 0.0000% | 0.0000% | 0.1314% | 0.0000% | 0.0000% | 0.0910% | 0.0000% | 0.0000% |
| MARTINSVILLE CITY | 9070 | 0.0992% | 0.0000% | 0.0000% | 0.0882% | 0.0000% | 0.0000% | 0.0992% | 0.0000% | 0.0000% | 0.0882% | 0.0000% | 0.0000% |
| MIDDLESEX COUNTY | 8746 | 0.1029% | 0.0114% | 0.0000% | 0.0800% | 0.0000% | 0.0000% | 0.1029% | 0.0114% | 0.0000% | 0.0800% | 0.0000% | 0.0000% |
| POQUOSON CITY | 9635 | 0.0934% | 0.0000% | 0.0000% | 0.0934% | 0.0000% | 0.0000% | 0.0934% | 0.0000% | 0.0000% | 0.0934% | 0.0000% | 0.0000% |
| ROANOKE CITY | 66083 | 0.0817% | 0.0015% | 0.0000% | 0.0666% | 0.0000% | 0.0000% | 0.0817% | 0.0015% | 0.0000% | 0.0666% | 0.0000% | 0.0000% |
| RUSSELL COUNTY | 19240 | 0.1091% | 0.0000% | 0.0000% | 0.1040% | 0.0000% | 0.0000% | 0.1091% | 0.0000% | 0.0000% | 0.1040% | 0.0000% | 0.0000% |