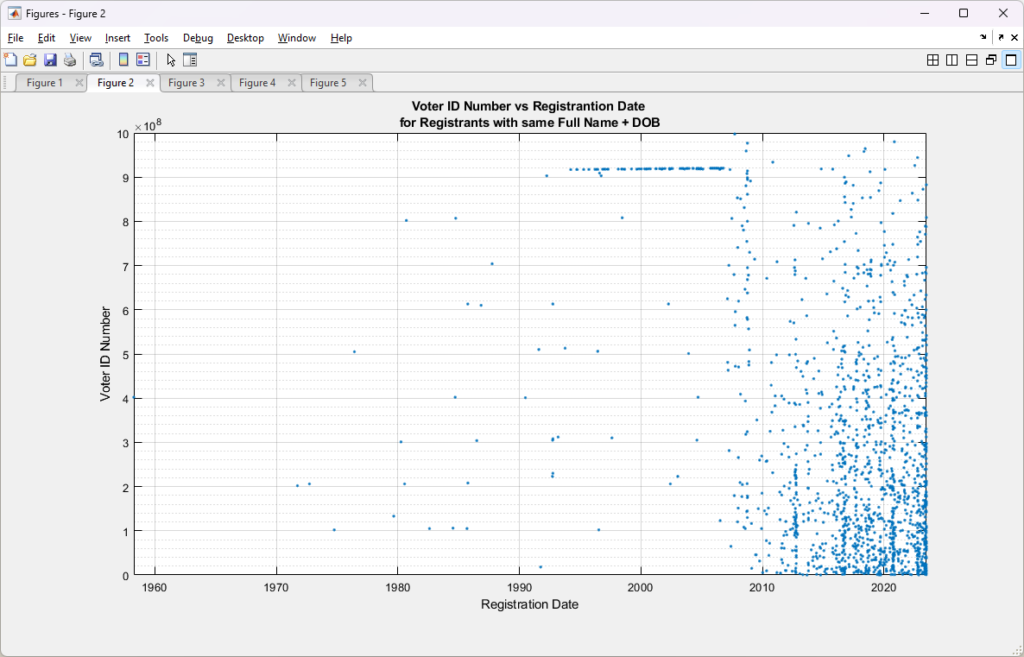
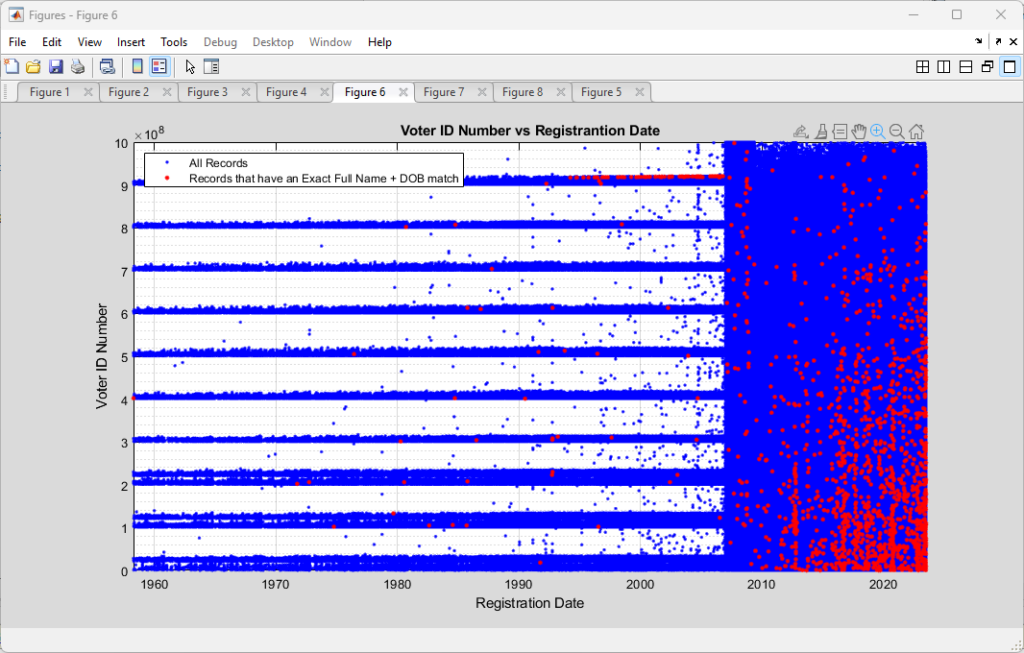
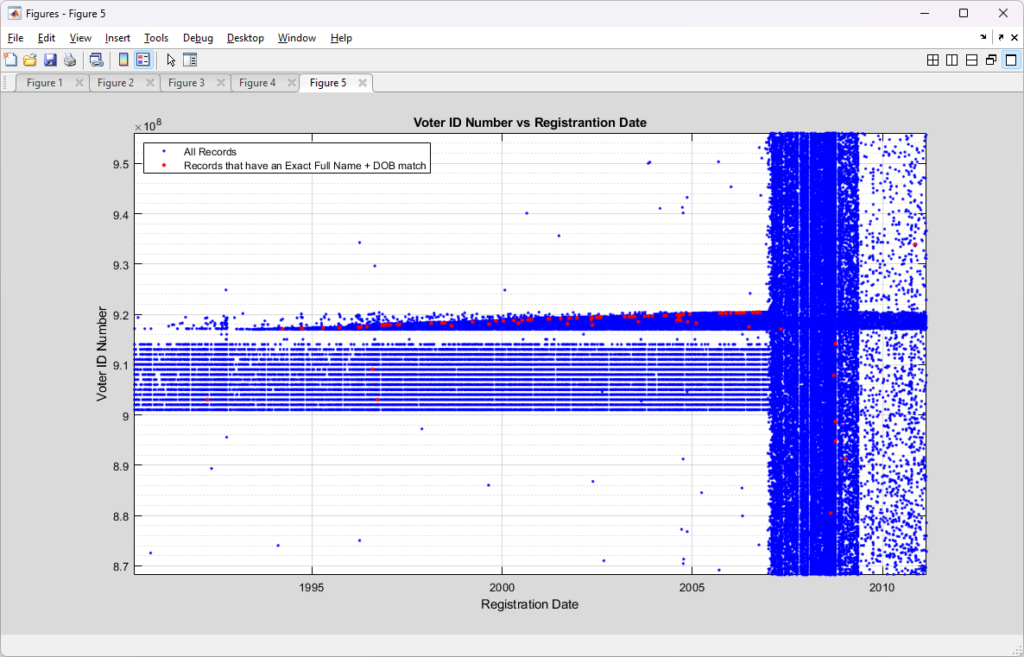
Recently I was made aware of the work Ed Solomon had been doing with data from the 2020 Colorado Cast Vote Records (CVRs), and I’ve taken some time to replicate and validate some of his data observations. I don’t always agree with Ed, but I wanted to take some time and verify the facts of the matter for myself.
For background, CVRs are machine logs of the way the tabulators process the “cast” ballots. You can think of them as equivalent to your bank statement showing all of the recorded transactions for each ballot scanned. They are required to be producible by ballot electronic tabulation systems, and are used as part of official forensic audits and documentation. They do not have any personal information and simply operate on the content of individual ballots as they are processed.
There are 2 specific items that need to be validated here:
- Odd statistics associated with statewide ballot measures in Arapahoe County as compared to other counties. Specifically, there were two statewide ballot measures (one dealing with taxes, and another on abortion) that one would expect to show a significant partisan split, and we in fact do see such a split in neighboring El Paso and Adams counties. However, the ballot measures do not show the partisan split in Arapahoe County.
- The difference is not just that the partisan split is muted or reduced, it is a night and day difference. In Arapahoe county there is almost no statistical difference between Trump and Biden voters on the ballot measures, but there is an obvious and clear difference on the same ballot measures in neighboring Adams and El Paso counties.
- Why is this important? It raises questions as to the veracity of the election counts, data handling practices, and the ability to use CVRs for their intended forensic purpose.
- The fact that the Arapahoe County CVR data was changed on the official county website without any notification or explanation around Feb 2025. The internal composition of ballots was changed in the data and “scrambled” by Arapahoe county … with the new version of the CVR files no longer showing the inconsistency from #1.
- As CVRs are official records that are used for legal purposes such as audits etc., they should never be “quietly” changed or modified retroactively. A full and transparent explanation of the issues and steps made to remedy should accompany any updates for official documents such as CVRs.
- This change took place years after the CVR was originally produced, and after Ed Solomon had used this particular CVR as part of his supporting documentation in an election case (Thompson vs Secretary of State NV) in Nevada.
- After Ed and Mark noticed the retroactive modifications and started asking questions, the County released a statement explaining that they were contacted by a researcher about potential issues with their CVR regarding “redaction” and privacy concerns.
- However, the county statement gives an incompatible date for when the documents were “corrected”, according to the file timestamps and internet archive logs. The statement claims April 2nd 2025, whereas the contents of the uploaded file show Feb 20th 2025 as the file modification date.
- The counties explanation does not comport with the observation of the scrambling of internal contents of official ballots. Its not just that the ordering of ballots was randomized to assuage privacy concerns, but that the actual records of votes cast were being swapped between ballots.
- At BEST this shows a woeful lack of transparency and procedural safeguards by the county.
- At WORST this has the appearance of being intentional tampering with official records.
I can independently replicate and validate both of these data observations. There does seem to be an issue with the ballot measures in the original Arapahoe County CVR data, and that data has been retroactively modified by the county in such a way as to scramble the information associated with votes cast.
Note that Ed Solomon, Draza Smith, Jeff O’Donnell (a.k.a. “The Lone Raccoon”), Mark Cook, MadLiberals, and others all provided data and pointers to the original documents and URLs in question, as well as their own analysis on the X.com platform.
Starting with item # 1:
Arapahoe County makes their CVR data available on their website (https://arapahoevotes.gov/transparency/). To obtain the new (modified) file click on the “Certification & Recounts” tab and scroll down to find the CVR link on the left hand side. Direct link is here: https://www.arapahoevotes.gov/file/2020-general-election-redacted-cast-vote-record
The original data is also still available on the Arapahoe County website, but one needs to do some creative sleuthing via the wayback machine and looking at the URL links in order to get to it, as was done by Mark Cook. (see: here and here)
The link to the original CVR file is: https://gis.arapahoegov.com/DL_Data/Redacted_CVR/Redacted_CVR_Export.zip
The original data from the 2020 CVR data had also been collected and collated by Jeff O’Donnell on his https://votedatabase.com (formerly ordros.com) site, which I archived and versioned in Sept of 2022. I can confirm that the original file matches the files in the votedatabase archive, as well as the current votedatabase site. I used additional files from votedatabase archive for neighboring Adams and El Paso counties as a source for the rest of this work, as I could not find corresponding links to CVR downloads on the Adams or El Paso county websites.
Ed’s original observation was that the two ballot measures that *should* be partisan split were not when looking at the original 2020 CVR Arapahoe County data. He used this observation as supporting evidence showing inconsistencies and irregularities in 2020 election data in an court case (Thompson vs Secretary of State NV) he was providing analysis for in Nevada. All of his analysis and the original file have therefore been previously submitted to the court.
Amendment B was a repeal of the “Gallagher Amendment” dealing with property tax rates and was expected to have a highly partisan split. Likewise Proposition 115 dealt with abortion and was also expected to have highly partisan split.
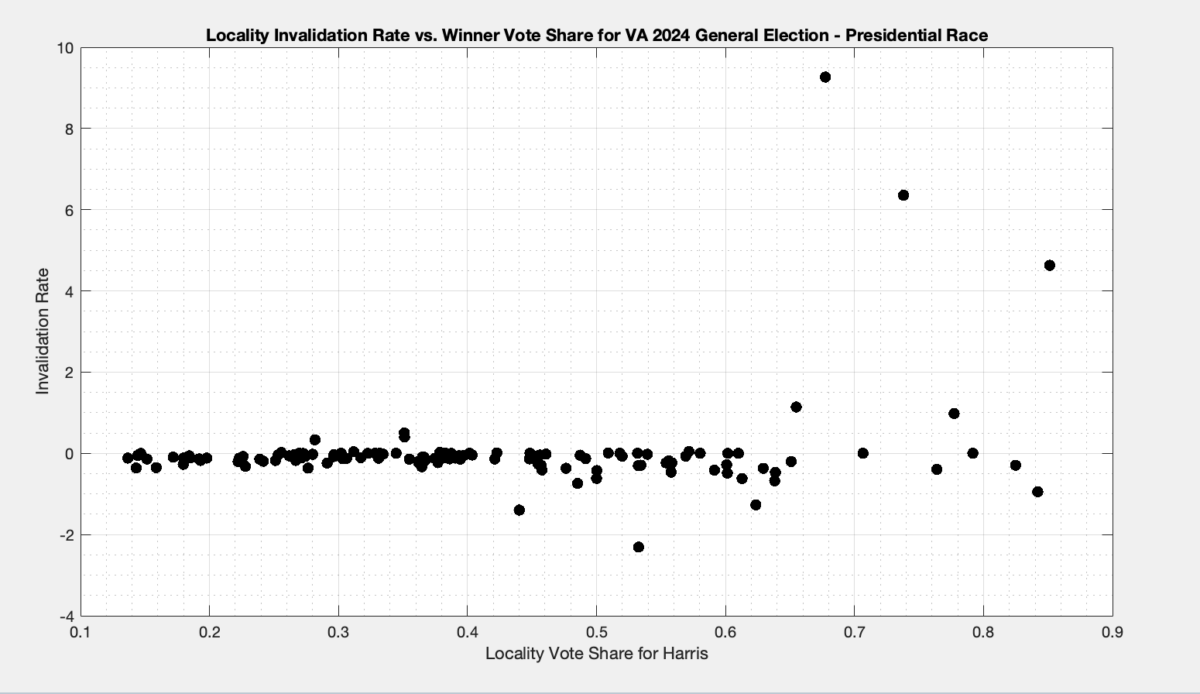
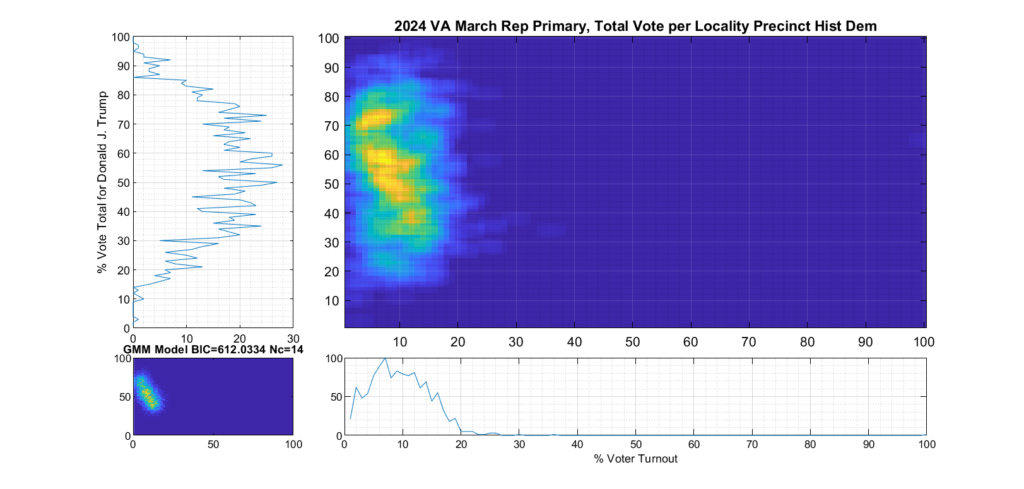
If we look at the plots of the ballots cast for these two ballot measures, but we condition them on if the person voted for Trump or Biden at the top of the ticket we do see in neighboring counties such as El Paso and Adams counties this partisan split, as shown below. Note the significant spread between the Biden/No (Yellow) & Trump/No (Purple), as well as between the Biden/Yes (Blue) & Trump/Yes (Red).
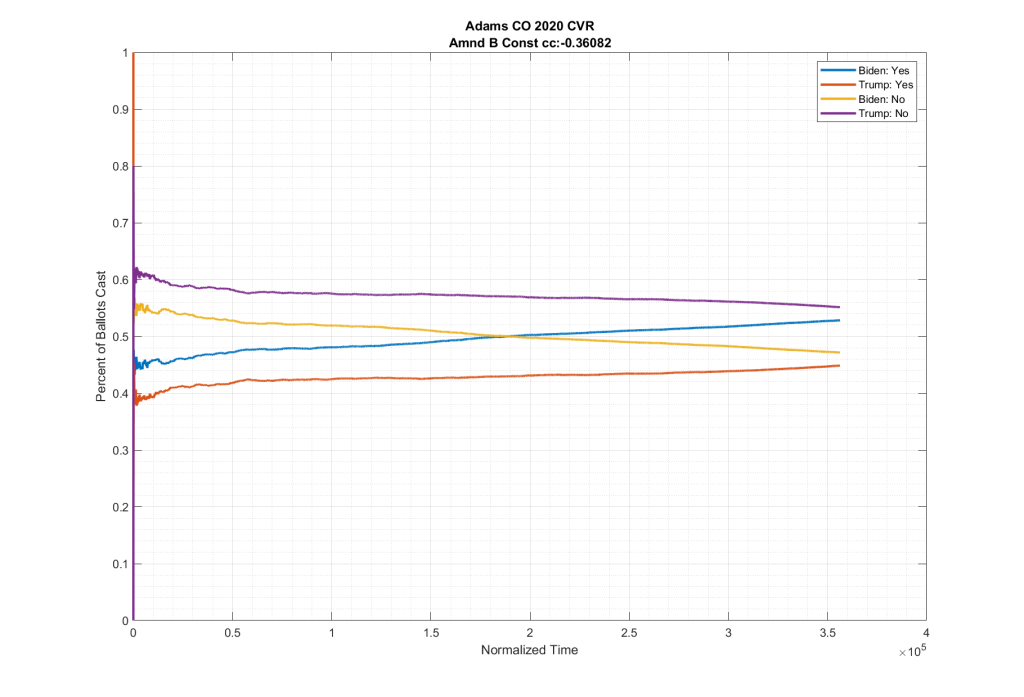
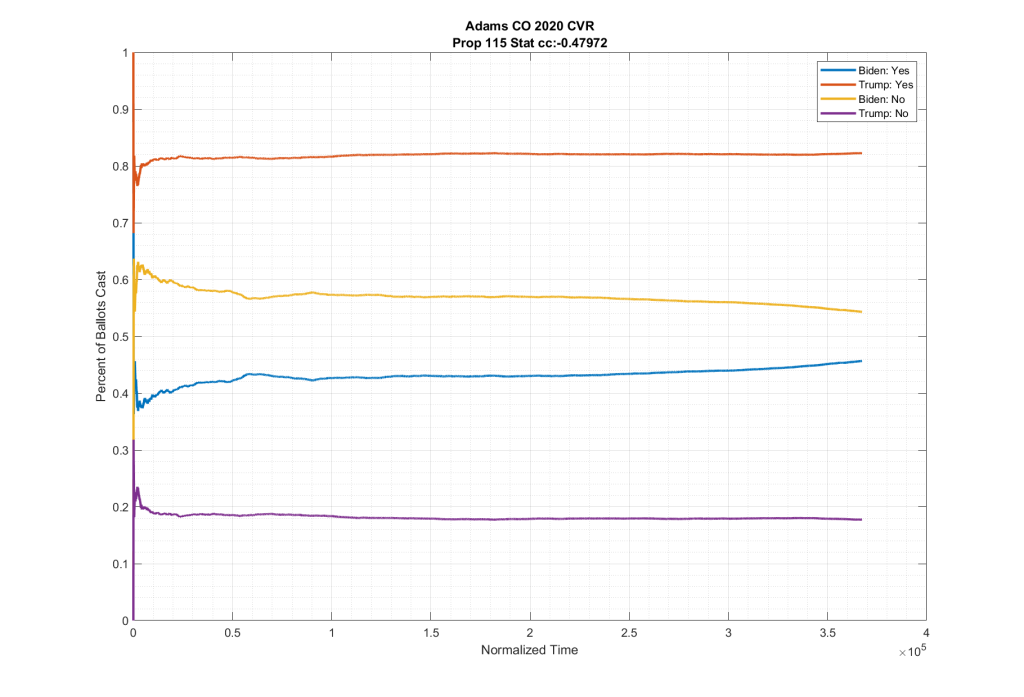
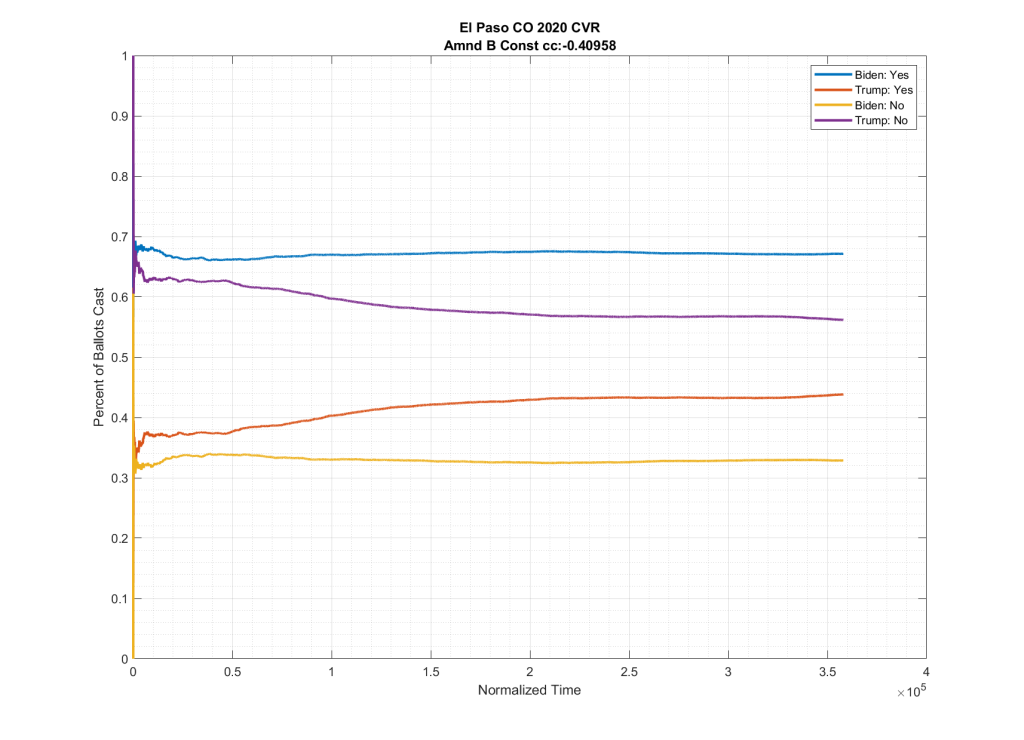
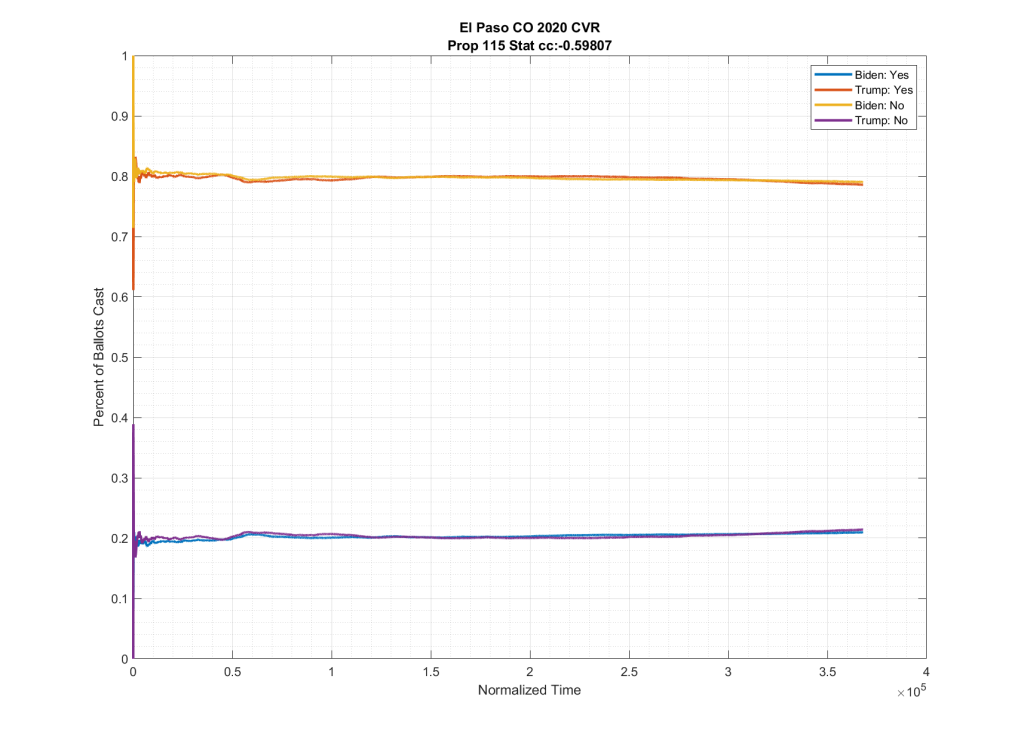
As can be seen in the plots above from Adams and El Paso counties, there is a significant partisan split in these two down-ballot races when conditioned on how the top of the ticket votes. However this seems to vanish when looking at Arapahoe County, with the Biden/No (Yellow) & Trump/No (Purple) and the Biden/Yes (Blue) & Trump/Yes (Red) stacking almost completely on top of one another.
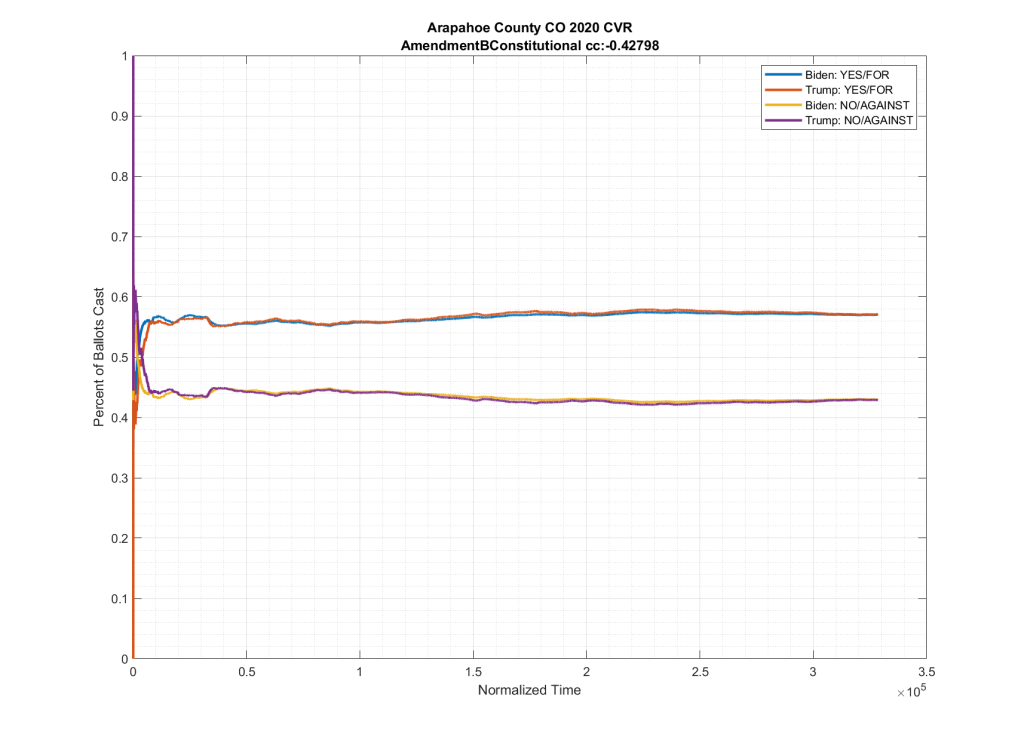
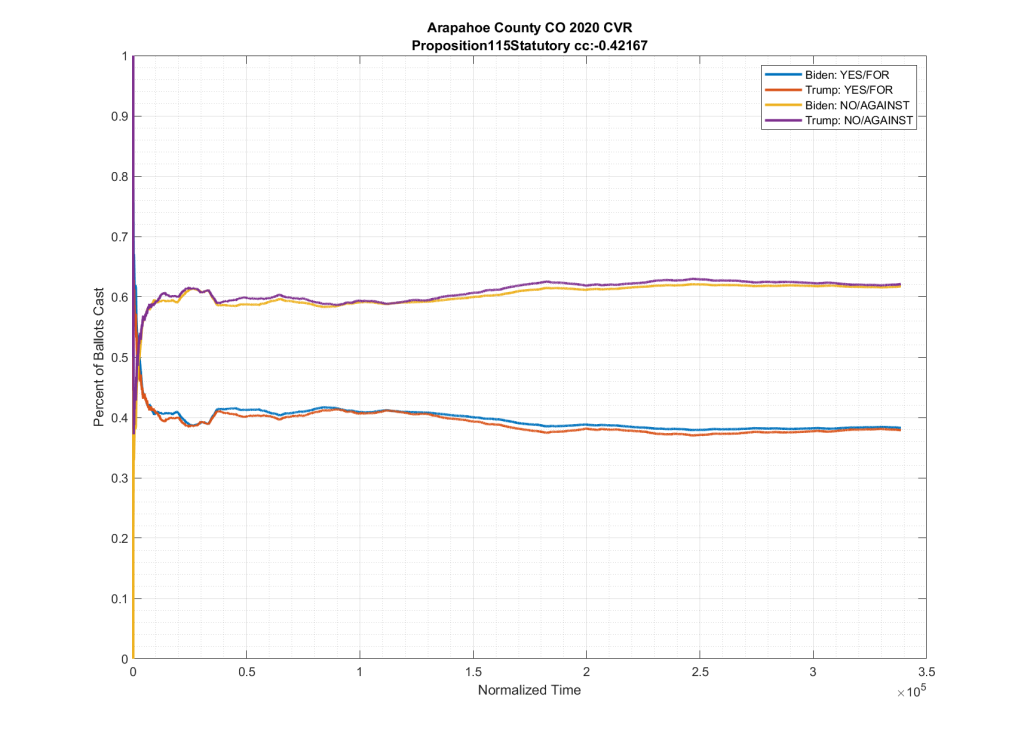
It can be clearly seen in the plots that the partisan split that was present in the other counties results seems to have completely vanished in Arapahoe.
I will note that the partisan split seems to be missing from almost all down-ballot races that I looked at, not just these two, although these were the ones specifically called out by Ed. This is an important point that I will come back to in a minute.
… And now to item # 2:
Ed’s original observation was submitted as part of his case in Nevada. At one point he and Mark Cook attempted to make a live stream video showing how people could recreate the observations starting from the source documents on the Arapahoe County website, which is when he and Mark realized that the original CVR file on the county website had been quietly replaced with a new file that had its contents scrambled and the results no longer showed the observed pattern.
Note that a CVR file is a legally required forensic record. It is the equivalent of a bank transaction log, and should almost never have its contents manipulated. If an error is discovered, and a correction does need to be issued, then a new file with the corrections should be published along side the original with a clear and prominent explanation and notification of the change. In this case, however, the County simply replaced the link to the original file with the new file with no explanation and no notice.
It was only after this was discovered, and after Ed started making phone calls to the County and bringing up the issue with the Judge in his Nevada case, that Arapahoe County belabouredly published an admission that they had adjusted the file. Their excuse for the modification was that they were made aware of a mistake with their “redaction” of data in the original publication, and were worried about individual privacy.
The (new) altered file did have 16 specific ballots that had their down-ballot races zeroed out, and was missing the “CountingGroup” metadata column. However, the file didn’t just have a small number of ballots (16) down-ballot information omitted, the internal contents on ALL ballots were also completely scrambled, with the top-of-the-ticket entries for President and Senate and metadata columns being completely reordered from all of the down-ballot information. This split-scrambling also also “fixed” the observed issues with Amendment B and Proposition 115, as can be seen below, where there is now a distinct partisan split between the data trends.


This kicked off multiple efforts to reverse engineer the actual changes that were performed on the CVR data by Arapahoe county, by myself and multiple others. Jeff O’Donnell and MadLiberals on X made the observation of the split reordering. I was able to verify this and remove the split-shuffling, exposing the fact that there were 16 ballots that also had all of their down ballot information zeroed out. There were a total of 432 down ballot votes that were removed from 16 specific ballots, followed by ALL of the President and Senate votes for ALL ballots being scrambled in relation to their down-ballot races.
Back to the point I made before above … the “scrambling” of the new file does seem to have “fixed” the expected partisan nature of most of the down-ballot races, so it is not unreasonable to think that this was actually a “fix” for a processing error on the original CVR file. That being said, the original (assumed incorrect) CVR was used in an audit process of two down-ballot races (linked above). Why did they not catch this issue years earlier during the audit? And why did they make the change to files, under the pretense of privacy issues, without announcing and documenting the errors?
Conclusion:
I can verify the two main data issues documented by Ed Solomon on the Arapahoe County 2020 CVR data.
The original data file had significant issues with down-ballot races not showing the expected partisan splits.
Arapahoe county did “quietly” revise the data without explanation until it was discovered by Ed and Mark, and then when pushed, only acknowledged that there was an issue with redactions and data privacy concerns.
The fact that the modification did correct the expected partisan split for ALL down-ballot races lends some credence to the assertion that they were correcting an error/issue with the original CVR file, however it does not excuse the fact that they performed this correction without notice or explanation. It also does not explain how their 2020 audit was able to use the incorrect original CVR files and not catch any of these issues.
The CVR files are intended to be official forensic records. If they are subject to manipulation and “adjustments” without transparency then that brings into question the validity of those files as forensic devices in the first place.
Corrections:
- (5/28/2025) Typo correction in that the original posting of this article had “April 2 2024” as the data the Arapahoe county statement said they changed the CVR. That was corrected to be “April 2 2025”.
- (5/28/2025) I had the wrong reference for the associated case in NV. I had originally posted that the case was the “Gilbert” case. It is actually “Thompson vs State”. Links have been updated accordingly.
- (5/28/2025) Minor spelling errors corrected.