Category: Election Integrity

Compiled per precinct data for VA 2020 and 2021

Post author By Jonathan Lareau
Post date December 12, 2021

Below I’ve linked copies of newly compiled sets of VA 2020 President and 2021 Governor November General Election data for anybody who is interested. The data set is compiled from only official VA Dept of Elections data sources including the General Election CSV files, the turnout CSV files, and the Daily Absentee List for each election.

Columns common to all source data:

“LOCALITY” – Locality Name
“DISTRICT” – Congressional district ID number
“PRECINCT_ID” – Precinct ID number
“PRECINCT” – Precinct Name

Columns compiled from the General Election CSV file:

“Democratic” – Number of Democratic Party Votes
“Liberation” – Number of Liberation Party Votes
“Republican”- Number of Republican Party Votes
“UNDEFINED” – Number of Write in Votes
“TOTAL_VOTES” – Sum of [“Democratic”, “Liberation”, “Republican”, “UNDEFINED”]

Columns compiled from the Turnout CSV file:

“PROVISIONAL_BALLOTS” – Number of Provisional Ballots
“ABSENTEE_BALLOTS” – Number of Absentee Ballots
“CURBSIDE_BALLOTS” – Number of Curbside Ballots
“ABS_OR_CURB_BALLOTS” – Sum of [“ABSENTEE_BALLOTS”, “CURBSIDE_BALLOTS”]
“TOTAL_VOTE_TURNOUT” – Total number of ballots coollected
“ACTIVE_REGISTERED_VOTERS” – The number of active voters
“TOTAL_REGISTERED_VOTERS” – The total number of registered voters

Columns compiled from the DAL file:

“ABSENTEE_ISSUED” – Number of approved but outstanding “Issued” ballots listed in the DAL
“ABSENTEE_MARKED” – Number of approved ballots listed as “Marked” in the DAL
“ABSENTEE_PRE_PROCESSED” – Number of approved ballots listed as “Pre-Processed” in the DAL
“ABSENTEE_MRKORPRE” – Sum of [“ABSENTEE_MARKED”, “ABSENTEE_PRE_PROCESSED”]
“ABSENTEE_EARLY_IN_PERSON” – Number of approved ballots listed as “On Machine” in the DAL
“ABSENTEE_FWAB” – Number of approved ballots listed as “FWAB” in the DAL
“ABSENTEE_COUNTABLE” – Sum of [“ABSENTEE_MARKED”, “ABSENTEE_PRE_PROCESSED”, “ABSENTEE_EARLY_IN_PERSON”, “ABSENTEE_FWAB”]

Columns created by summing all entries in a locality:

“TOTAL_VOTES_IN_LOCALITY”
“ACTIVE_REGISTERED_VOTERS_IN_LOCALITY”
“TOTAL_REGISTERED_VOTERS_IN_LOCALITY”
“ABSENTEE_ISSUED_IN_LOCALITY”
“ABSENTEE_MARKED_IN_LOCALITY”
“ABSENTEE_PRE_PROCESSED_IN_LOCALITY”
“ABSENTEE_MARKED_OR_PRE_IN_LOCALITY”
“ABSENTEE_EARLY_IN_PERSON_IN_LOCALITY”
“ABSENTEE_FWAB_IN_LOCALITY”
“ABSENTEE_COUNTABLE_IN_LOCALITY”

compiled_VA_2020_data_v2021-12-12 Download

compiled_VA_2021_data_v2021-12-12 Download

Source Data Files (except DAL):

2020-November-General-v11-10-2020 Download

Turnout-2020-November-General-v11-30-2020 Download

Turnout-2021-November-General-v12-12-2021 Download

2021-November-General Download

Election Data Analysis Election Forensics Election Integrity programming technical

VHL, RVL and DAL metrics for VA 2021 and (2020) General Elections

Post author By Jonathan Lareau
Post date December 12, 2021

As I now have available the Registered Voter List (RVL), the Voter History List (VHL) and the completed Daily Absentee List (DAL) files for the 2020 and 2021 VA November General elections, I did some basic metrics computations on these files for those that are interested. The Voter History and Registered Voter List files used to generate these results were downloaded from VA Dept of Elections on 2021-12-11. The 2021 DAL file used was downloaded 2021-12-05. The 2020 DAL file was downloaded 2020-11-09.

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Basic Voter History and Registered Voter List Metrics
nInPDayOf2020 = 1638026 
nAbs2020 = 2734048 
nInPAbsOf2020 =  657 

nInPDayOf2021 = 1721868 
nAbs2021 = 1188842 
nInPAbsOf2021 = 0 

nUniqueVHIDs = 4769508 
nUniqueRVLIDs = 5956464 
nIntersectUVVHwURVL = 4769508 

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Ages of the registered voters at the time of the election from RVL
regv_over100_On2021Elect = 2736 
regv_regv_lessThan18_On2021Elect = 397 
regv_over100_On2020Elect = 1774 
regv_lessThan18_On2020Elect = 43939 
regv_lessThan17_On2020Elect = 391

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Ages of the registered voters at the time of the election from VHL
vh_over100_On2021Elect = 514 
vh_lessThan18_On2021Elect = 0 
vh_over100_On2020Elect = 558 
vh_lessThan18_On2020Elect = 1 
vh_lessThan17_On2020Elect = 0

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Do some basic indexing of different DAL status categories and combinations
nApprovedAndIssued2021 = 58151 
nApprovedAndMarked2021 = 78278 
nApprovedAndOnMachine2021 = 861470 
nApprovedAndPreProcessed2021 = 254374 
nApprovedAndFWAB2021 = 52 
nApprovedAndCountable2021 = 1194174 

nApprovedAndIssued2020 = 106037 
nApprovedAndMarked2020 = 348705 
nApprovedAndOnMachine2020 = 1796973
nApprovedAndPreProcessed2020 = 670765
nApprovedAndFWAB2020 = 1351
nApprovedAndCountable2020 = 2817794

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many countable entries in the 2021 dal are not contained in the voter
% registraion file for 2021
phantomDALVoters2021 = 0

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many countable entries in the 2020 dal are not contained in the voter
% registraion file for 2021
phantomDALVoters2020 = 48721

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many approved but not counted entries in the 2020 dal are not
% contained in the voter registraion file for 2021?  
phantomDALBallots2020 = 3671

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were issued but not counted or spoiled AND the
% person is marked as having voted in person on election day
% For 2020:
numUnspoiled2020 = 106037
numUnspoiledAndInPDayOf2020 = 35806

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were issued but not counted or spoiled AND the
% person is marked as having voted in person on election day
% For 2021:
numUnspoiled2021 = 58151
numUnspoiledAndInPDayOf2021 = 4632

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were approved and counted AND the
% person is marked as having voted IN PERSON on election day. (Should be 0)
% For 2020:
numCountedAbs2020 = 2817794
numCountedAbs2020AndInPDayOf2020 = 245

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were approved and counted AND the
% person is marked as having voted IN PERSON on election day. (Should be 0)
% For 2021:
numCountedAbs2021 = 1194174
numCountedAbs2021AndInPDayOf2021 = 14

The MATLAB program listing for generating these metrics is below. I have left off the parsing routines that parse the various csv input files into MATLAB Table objects. Text highlighted in BOLD is the computed metric results as listed above.

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Basic Voter History and Registered Voter List Metrics
inPDayOf2020 = VAVoteHistory.ELECTION_NAME=='2020 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2020 & ...
    VAVoteHistory.ABSENTEE == 'False';
abs2020 = VAVoteHistory.ELECTION_NAME=='2020 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2020 & ...
    VAVoteHistory.ABSENTEE == 'True';
inPAbsOf2020 = VAVoteHistory.ELECTION_NAME=='2020 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2020 & ...
    VAVoteHistory.ABSENTEE == 'True' & VAVoteHistory.VOTE_IN_PERSON=='True';
nInPDayOf2020 = sum(inPDayOf2020)
nAbs2020 = sum(abs2020)
nInPAbsOf2020 = sum(inPAbsOf2020)
inPDayOf2021 = VAVoteHistory.ELECTION_NAME=='2021 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2021 & ...
    VAVoteHistory.ABSENTEE == 'False';
abs2021 = VAVoteHistory.ELECTION_NAME=='2021 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2021 & ...
    VAVoteHistory.ABSENTEE == 'True';
inPAbsOf2021 = VAVoteHistory.ELECTION_NAME=='2021 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2021 & ...
    VAVoteHistory.ABSENTEE == 'True' & VAVoteHistory.VOTE_IN_PERSON=='True';
nInPDayOf2021 = sum(inPDayOf2021)
nAbs2021 = sum(abs2021)
nInPAbsOf2021 = sum(inPAbsOf2021)
uvhid = unique(VAVoteHistory.IDENTIFICATION_NUMBER);
urvlid = unique(RegisteredVoterList.IDENTIFICATION_NUMBER);
nUniqueVHIDs = numel(uvhid)
nUniqueRVLIDs = numel(urvlid)
intersectUVVHwURVL = intersect(uvhid,urvlid);
nIntersectUVVHwURVL = numel(intersectUVVHwURVL)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Ages of the registered voters at the time of the election from RVL
dob = datenum(RegisteredVoterList.DOB);
ageOn2021Elect = (datenum("11/03/2021") - dob) / 365.25;
ageOn2020Elect = (datenum("11/04/2020") - dob) / 365.25;

regv_over100_On2021Elect = sum(ageOn2021Elect > 100)
regv_lessThan18_On2021Elect = sum(ageOn2021Elect < 18)
regv_over100_On2020Elect = sum(ageOn2020Elect > 100)
regv_lessThan18_On2020Elect = sum(ageOn2020Elect < 18)
regv_lessThan17_On2020Elect = sum(ageOn2020Elect < 17)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Ages of the registered voters at the time of the election from VHL
vh2021 = VAVoteHistory.ELECTION_NAME=='2021 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2021;
vh2020 = VAVoteHistory.ELECTION_NAME=='2020 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2020;
dob_vh = datenum(VAVoteHistory.DOB);
ageOn2021Elect_vh = (datenum("11/03/2021") - dob_vh) / 365.25;
ageOn2020Elect_vh = (datenum("11/04/2020") - dob_vh) / 365.25;

vh_over100_On2021Elect = sum(ageOn2021Elect_vh(vh2021) > 100)
vh_lessThan18_On2021Elect = sum(ageOn2021Elect_vh(vh2021) < 18)
vh_over100_On2020Elect = sum(ageOn2020Elect_vh(vh2020) > 100)
vh_lessThan18_On2020Elect = sum(ageOn2020Elect_vh(vh2020) < 18)
vh_lessThan17_On2020Elect = sum(ageOn2020Elect_vh(vh2020) < 17)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Do some basic indexing of different DAL status categories and combinations
aiv2021 = dal2021.APP_STATUS == 'Approved' & dal2021.BALLOT_STATUS == 'Issued';
amv2021 = dal2021.APP_STATUS == 'Approved' & dal2021.BALLOT_STATUS == 'Marked';
aomv2021 = dal2021.APP_STATUS == 'Approved' & dal2021.BALLOT_STATUS == 'On Machine';
appv2021 = dal2021.APP_STATUS == 'Approved' & dal2021.BALLOT_STATUS == 'Pre-Processed';
afwv2021 = dal2021.APP_STATUS == 'Approved' & dal2021.BALLOT_STATUS == 'FWAB';
appmv2021 = amv2021 | aomv2021 | appv2021 | afwv2021; % Approved and Countable

aiv2020 = dal2020.APP_STATUS == 'Approved' & dal2020.BALLOT_STATUS == 'Issued';
amv2020 = dal2020.APP_STATUS == 'Approved' & dal2020.BALLOT_STATUS == 'Marked';
aomv2020 = dal2020.APP_STATUS == 'Approved' & dal2020.BALLOT_STATUS == 'On Machine';
appv2020 = dal2020.APP_STATUS == 'Approved' & dal2020.BALLOT_STATUS == 'Pre-Processed';
afwv2020 = dal2020.APP_STATUS == 'Approved' & dal2020.BALLOT_STATUS == 'FWAB';
appmv2020 = amv2020 | aomv2020 | appv2020 | afwv2020; % Approved and Countable

nApprovedAndIssued2021 = sum (aiv2021)
nApprovedAndMarked2021 = sum (amv2021)
nApprovedAndOnMachine2021 = sum (aomv2021)
nApprovedAndPreProcessed2021 = sum (appv2021)
nApprovedAndFWAB2021 = sum (afwv2021)
nApprovedAndCountable2021 = sum (appmv2021)

nApprovedAndIssued2020 = sum (aiv2020)
nApprovedAndMarked2020 = sum (amv2020)
nApprovedAndOnMachine2020 = sum (aomv2020)
nApprovedAndPreProcessed2020 = sum (appv2020)
nApprovedAndFWAB2020 = sum (afwv2020)
nApprovedAndCountable2020 = sum (appmv2020)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many countable entries in the 2021 dal are not contained in the voter
% registraion file for 2021?
ua = unique(string(dal2021.identification_number(appmv2021)));
ub = unique(string(RegisteredVoterList.IDENTIFICATION_NUMBER));
[uc,ia,ib] = intersect(ua,ub);
phantomDALPct2021 = numel(uc) / numel(ua) * 100
phantomDALVoters2021 = numel(ua) - numel(uc)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many countable entries in the 2020 dal are not contained in the voter
% registraion file for 2021? 
[ua2020,ia,ic] = unique(string(dal2020.identification_number(appmv2020)));
ub2020 = unique(string(RegisteredVoterList.IDENTIFICATION_NUMBER));
[uc2020] = intersect(ua2020,ub2020);
phantomDALPct2020 = numel(uc2020) / numel(ua2020) * 100
phantomDALVoters2020 = numel(ua2020) - numel(uc2020)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many approved but not counted entries in the 2020 dal are not
% contained in the voter registraion file for 2021?  
[ua2020,ia,ic] = unique(string(dal2020.identification_number(aiv2020)));
ub2020 = unique(string(RegisteredVoterList.IDENTIFICATION_NUMBER));
[uc2020] = intersect(ua2020,ub2020);
phantomDALBallotsPct2020 = numel(uc2020) / numel(ua2020) * 100
phantomDALBallots2020 = numel(ua2020) - numel(uc2020)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were issued but not counted or spoiled AND the
% person is marked as having voted in person on election day
% For 2020:
unspoiled2020 = dal2020.identification_number(aiv2020);
ngIPDOidx = VAVoteHistory.ELECTION_NAME=='2020 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2020 & ...
    VAVoteHistory.ABSENTEE == 'False';
novGenInPersonDayOf2020 = VAVoteHistory.IDENTIFICATION_NUMBER(ngIPDOidx);
ua2020 = unique(unspoiled2020);
ub2020 = unique(novGenInPersonDayOf2020);
uc2020 = intersect(ua2020,ub2020);
numUnspoiled2020 = numel(unspoiled2020)
numUnspoiledAndInPDayOf2020 = numel(uc2020)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were issued but not counted or spoiled AND the
% person is marked as having voted in person on election day
% For 2021:
unspoiled2021 = dal2021.identification_number(aiv2021);
ngIPDOidx = VAVoteHistory.ELECTION_NAME=='2021 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2021 & ...
    VAVoteHistory.ABSENTEE == 'False';
novGenInPersonDayOf2021 = VAVoteHistory.IDENTIFICATION_NUMBER(ngIPDOidx);
ua2021 = unique(unspoiled2021);
ub2021 = unique(novGenInPersonDayOf2021);
uc2021 = intersect(ua2021,ub2021);
numUnspoiled2021 = numel(unspoiled2021)
numUnspoiledAndInPDayOf2021 = numel(uc2021)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were approved and counted AND the
% person is marked as having voted IN PERSON on election day. (Should be 0)
% For 2020:
countedAbs2020 = dal2020.identification_number(appmv2020);
ngIPDOidx = VAVoteHistory.ELECTION_NAME=='2020 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2020 & ...
    VAVoteHistory.ABSENTEE == 'False';
novGenInPersonDayOf2020 = VAVoteHistory.IDENTIFICATION_NUMBER(ngIPDOidx);
ua2020 = unique(countedAbs2020);
ub2020 = unique(novGenInPersonDayOf2020);
uc2020 = intersect(ua2020,ub2020);
numCountedAbs2020 = numel(countedAbs2020)
numCountedAbs2020AndInPDayOf2020 = numel(uc2020)

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% How many absentee ballots were approved and counted AND the
% person is marked as having voted IN PERSON on election day. (Should be 0)
% For 2021:
countedAbs2021 = dal2021.identification_number(appmv2021);
ngIPDOidx = VAVoteHistory.ELECTION_NAME=='2021 November General' & ...
    VAVoteHistory.ELECTION_YEAR==2021 & ...
    VAVoteHistory.ABSENTEE == 'False';
novGenInPersonDayOf2021 = VAVoteHistory.IDENTIFICATION_NUMBER(ngIPDOidx);
ua2021 = unique(countedAbs2021);
ub2021 = unique(novGenInPersonDayOf2021);
uc2021 = intersect(ua2021,ub2021);
numCountedAbs2021 = numel(countedAbs2021)
numCountedAbs2021AndInPDayOf2021 = numel(uc2021)

Election Data Analysis Election Forensics Election Integrity Interesting programming technical Uncategorized

In-Person Early Vote records added after the close of Early Voting in VA 2021

Post author By Jonathan Lareau
Post date December 10, 2021

Note: there has been an update and follow up to this entry that you can read here.

BLUF: There were 4632 In-Person Early Vote records inserted into the Daily Absentee List (DAL) records after the close of early voting in VA in 2021. There is no plausible explanation as to why these records should have been legitimately added retrospectively that I am aware of.

The RPV and candidates were made aware of this information at the time of its discovery (~Nov 8th), but I specifically held off on publishing this information publicly until the candidates who wanted to contest or perform recounts had a chance to do so and that process was completed.

The Daily Absentee List (DAL) is a view of the status of Absentee and Early Vote ballots that is maintained by the Virginia Department of Elections and is available to qualified individuals, campaigns and organizations doing Get-Out-The-Vote (GOTV) efforts, etc. It is continuously updated over the course of an election, and is useful for tracking the number of Early and Absentee votes and their status as the early voting period is underway. Note that the DAL only tracks the status of early and absentee ballots, not the vote totals.

Through VA RPV candidates and PAC’s that I volunteer with, I was provided access to the DAL data for the 2021 election and I ran daily analysis and statistics on the DAL throughout the early voting period. That access came in the form of a link to a downloadable comma-seperated-value (csv) file from the Dept of Elections website. I downloaded snapshots of the DAL repeatedly over the election period, and I archived and time-stamped all of those downloads.

Important Dates:

The first day of Early Voting in VA was Sept 17, 2021.
The last day to register to vote in the VA 2021 elections was Oct 12, 2021.
The last day to request a by-mail absentee ballot was Oct 22, 2021.
The last day of Early Voting in VA was Oct 30, 2021.

Note that individuals can request mail-in absentee ballots prior to this date, but ballots do not get “Issued” and sent to the voter until the candidates and the ballot format has been finalized.

The DAL records are generated via the information in the poll-books at early voting stations, as well as through registrars and other election officials manually updating information with respect to mail-in absentee ballots. When a person is physically checked into an early voting site in order to vote early “On Machine”, their check-in information is updated and viewable (usually by the next day) in the DAL download. The DAL record will have a new entry with “APP_STATUS”=”Approved” and “BALLOT_STATUS”=”On Machine” for the voter when this occurs. The actual content of their ballot remains secret until the votes are counted after the close of the early voting period, when the scanning machines are closed out and their totals are computed and final reports are generated.

For Mail-In Absentee ballots the DAL records begin with the request for an absentee ballot. If the voter is qualified and the request is approved (“APP_STATUS”=”Approved”) a ballot is issued to the voter (“BALLOT_STATUS=”Issued”). When the ballot is returned to the registrar its “BALLOT_STATUS” is updated to “Marked”. When the ballot envelope is opened by elections staff and the ballot is scanned into a scanning machine, the “BALLOT_STATUS” is updated to “Pre-Processed”. The ballot record stays in this state until the early voting period ends and the vote totals are computed.

If a voter who previously requested a mail-in ballot decides to vote early in person, they must either bring their mail-in ballot with them to be spoiled or attest that they have lost or destroyed the ballot. The mail in ballot record is then cancelled and the in-person check-in and DAL records update occurs as above.

In figure 1 below we can see the summary of the DAL entries for VA House District 10 over time that illustrates this process. As time progresses we see a decrease in the amount of “Issued” ballots as well as corresponding changes in the “Marked” and “Pre-Processed” totals. Independently we see the in-person “On Machine” totals increasing until it stops changing after the early voting period ends (Oct 30th). Note that there is approximately a 1-2 day lag in my ability to observe these changes which is created from the combination of the discrete times that the DAL report file is generated on the VA servers, as well as the discrete times that I was polling the url link to grab these updated files. The “Issued”, “Marked” and “Pre-Processed” totals continue to be adjusted as the registrars office receives and processes mail in ballots.

Notice that the “OnMachine” trace of figure 1 flat-lines after Nov 1st. This is as expected, as all of the Early Voting sites have been closed up and there are no more people physically walking in, checking in on the poll books, and casting In-Person Early Votes. Note that the the “Day-Of” voting machines and poll-books are kept as separate systems and data records from the Early Vote systems.

As I was constantly producing and reprocessing these plots I noticed something interesting was occurring in various localities and precincts. Figure 2 below shows the same plot from State House District 097 (Hanover County). Everything looks fine until we see an uptick in the total number of “OnMachine” records in the DAL file that was pulled Nov 5 from the VA Dept of State weblink. I have had discussion with multiple elections officials and officers, and I have not yet been able to determine any legitimate reason for this uptick.

To dig in a little further I went back and reprocessed by House Congressional District all of the DAL data. Each of the DAL files has application receipt and ballot receipt dates associated with each “On Machine” entry. These two dates are the same for “On Machine” In Person Early Votes and correspond to the day that the person to cast their vote. I plotted all of the ballot receipt dates for each category of countable ballots (“On Machine”, “Marked”, “Pre-Processed” or “FWAB”) as well as the Application receive date of “Issued” ballots for each pulled DAL file and stitched these sequences together into movie sequences. The result for State House District 097 is shown below. Notice in the last few frames of the movie, corresponding to the bump in figure 2 above, we see that the DAL file gets injected with approximately 750 entries that have a “back-dated” receipt date of Oct 15 and the entire “On Machine” curve jumps accordingly. The still frames corresponding to the DAL files I downloaded at 2021-11-04 21:15:42 and 2021-11-05 09:44:23 are shown side by side in the gallery below the embedded movie.

We also see this large injection of backdated records in HD055 (also Hanover County) during the same DAL file update. But in this case the backdated ballots have a ballot receipt date that pre-dates the start of early voting. I’m not quite sure how people could have walked into an early voting precinct and checked into a poll book before the early voting precinct ever was setup or opened. The video sequence and the still images from 2021-11-04 21:15:42 and 2021-11-05 09:44:23 are again presented below.

Video of 055

If we try to look at all of the DAL file updates since Oct 31 (exclusive, to allow margin for data lag) we find that as of this writing there are 4632 new “Approved” and “On Machine” records that have been inserted into the DAL data since the close of early voting. Even more interesting is the distribution of the BALLOT_RECEIPT_DATE that has been applied to these additional records. We can see the large spike attributed to Oct 15th in Hanover County that originally caught my attention, but we also see a large number of dates that are before or after the early voting period, with an underlying exponential distribution during the valid early voting period.

There is no plausible legitimate explanation for these additions to the DAL records after the fact. This is unlikely to be a clerical or human error, as the syncing of “On Machine” records to the DAL database happens near realtime via the poll-book systems. This is not an isolated poll-book that wasn’t shut-down or syncing properly, as it is occurring throughout multiple localities and precincts. There is no explanation or justification for why these insertions would happen nearly a week after the end of the early voting period. There is no explanation or justification as to why the BALLOT_RECEIPT_DATE entries are outside of the legitimate early voting period.

I give the tallied distribution of these injected DAL records, by date of injection, by Locality, and by Precinct in the csv files and tables below for reference.

addedEntries_after_2021-10-31_summaryByDALfilename-1 Download

DAL Filename (Download Date & Time)	Number Of Injected “On Machine” DAL Records
Daily_Absentee_List_20211101T235927.csv	24
Daily_Absentee_List_20211102T235655.csv	37
Daily_Absentee_List_20211103T222822.csv	26
Daily_Absentee_List_20211104T211542.csv	578
Daily_Absentee_List_20211105T215045.csv	2039
Daily_Absentee_List_20211106T232716.csv	1928

addedEntries_after_2021-10-31_summaryByLocality Download

Locality Name	Number Of Injected “On Machine” DAL Records
LOUDOUN COUNTY	1515
HANOVER COUNTY	1310
ARLINGTON COUNTY	187
CHESAPEAKE CITY	99
HENRICO COUNTY	73
MONTGOMERY COUNTY	67
CHESTERFIELD COUNTY	59
YORK COUNTY	46
TAZEWELL COUNTY	45
FAIRFAX COUNTY	37
KING GEORGE COUNTY	37
WASHINGTON COUNTY	35
GLOUCESTER COUNTY	34
SHENANDOAH COUNTY	34
CHARLOTTESVILLE CITY	33
BOTETOURT COUNTY	30
PULASKI COUNTY	30
FREDERICKSBURG CITY	29
GILES COUNTY	29
NORTHAMPTON COUNTY	29
PRINCE WILLIAM COUNTY	29
ROCKINGHAM COUNTY	28
NEWPORT NEWS CITY	26
NORFOLK CITY	26
WINCHESTER CITY	24
FREDERICK COUNTY	23
CAROLINE COUNTY	21
ROANOKE COUNTY	21
VIRGINIA BEACH CITY	21
RUSSELL COUNTY	19
STAFFORD COUNTY	19
SUFFOLK CITY	19
MANASSAS CITY	18
CAMPBELL COUNTY	17
FAUQUIER COUNTY	17
RICHMOND CITY	16
LANCASTER COUNTY	15
ORANGE COUNTY	15
WILLIAMSBURG CITY	15
SPOTSYLVANIA COUNTY	14
COLONIAL HEIGHTS CITY	13
MECKLENBURG COUNTY	13
PRINCE EDWARD COUNTY	13
PRINCE GEORGE COUNTY	13
WARREN COUNTY	13
APPOMATTOX COUNTY	12
AUGUSTA COUNTY	12
LYNCHBURG CITY	12
ISLE OF WIGHT COUNTY	11
JAMES CITY COUNTY	11
WISE COUNTY	11
GOOCHLAND COUNTY	10
PORTSMOUTH CITY	10
ACCOMACK COUNTY	9
ALBEMARLE COUNTY	9
BRISTOL CITY	9
ESSEX COUNTY	9
HALIFAX COUNTY	9
LOUISA COUNTY	9
ROCKBRIDGE COUNTY	9
CARROLL COUNTY	8
DINWIDDIE COUNTY	8
HARRISONBURG CITY	8
ALEXANDRIA CITY	7
AMELIA COUNTY	7
FALLS CHURCH CITY	7
GREENSVILLE COUNTY	7
HAMPTON CITY	7
HOPEWELL CITY	7
KING WILLIAM COUNTY	7
HENRY COUNTY	6
LUNENBURG COUNTY	6
MATHEWS COUNTY	6
NELSON COUNTY	6
NORTHUMBERLAND COUNTY	6
ROANOKE CITY	6
AMHERST COUNTY	5
BEDFORD COUNTY	5
CHARLES CITY COUNTY	5
CLARKE COUNTY	5
EMPORIA CITY	5
FLUVANNA COUNTY	5
FRANKLIN COUNTY	5
GRAYSON COUNTY	5
GREENE COUNTY	5
PITTSYLVANIA COUNTY	5
POWHATAN COUNTY	5
ALLEGHANY COUNTY	4
BATH COUNTY	4
BUCHANAN COUNTY	4
BUCKINGHAM COUNTY	4
CHARLOTTE COUNTY	4
CUMBERLAND COUNTY	4
RAPPAHANNOCK COUNTY	4
WYTHE COUNTY	4
BRUNSWICK COUNTY	3
DICKENSON COUNTY	3
FAIRFAX CITY	3
FRANKLIN CITY	3
MIDDLESEX COUNTY	3
POQUOSON CITY	3
RADFORD CITY	3
STAUNTON CITY	3
SUSSEX COUNTY	3
WAYNESBORO CITY	3
WESTMORELAND COUNTY	3
CULPEPER COUNTY	2
DANVILLE CITY	2
FLOYD COUNTY	2
KING & QUEEN COUNTY	2
NOTTOWAY COUNTY	2
PATRICK COUNTY	2
PETERSBURG CITY	2
SALEM CITY	2
SOUTHAMPTON COUNTY	2
BLAND COUNTY	1
COVINGTON CITY	1
HIGHLAND COUNTY	1
LEXINGTON CITY	1
MADISON COUNTY	1
NORTON CITY	1
SMYTH COUNTY	1

addedEntries_after_2021-10-31_summaryByPrecinct Download

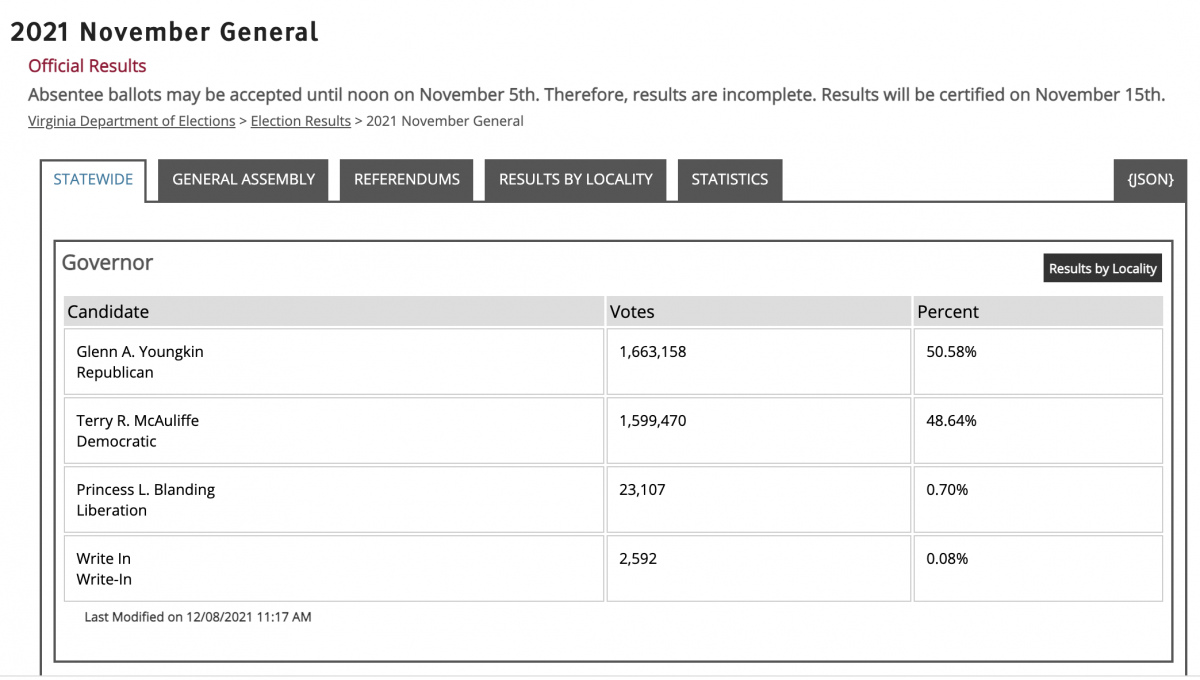
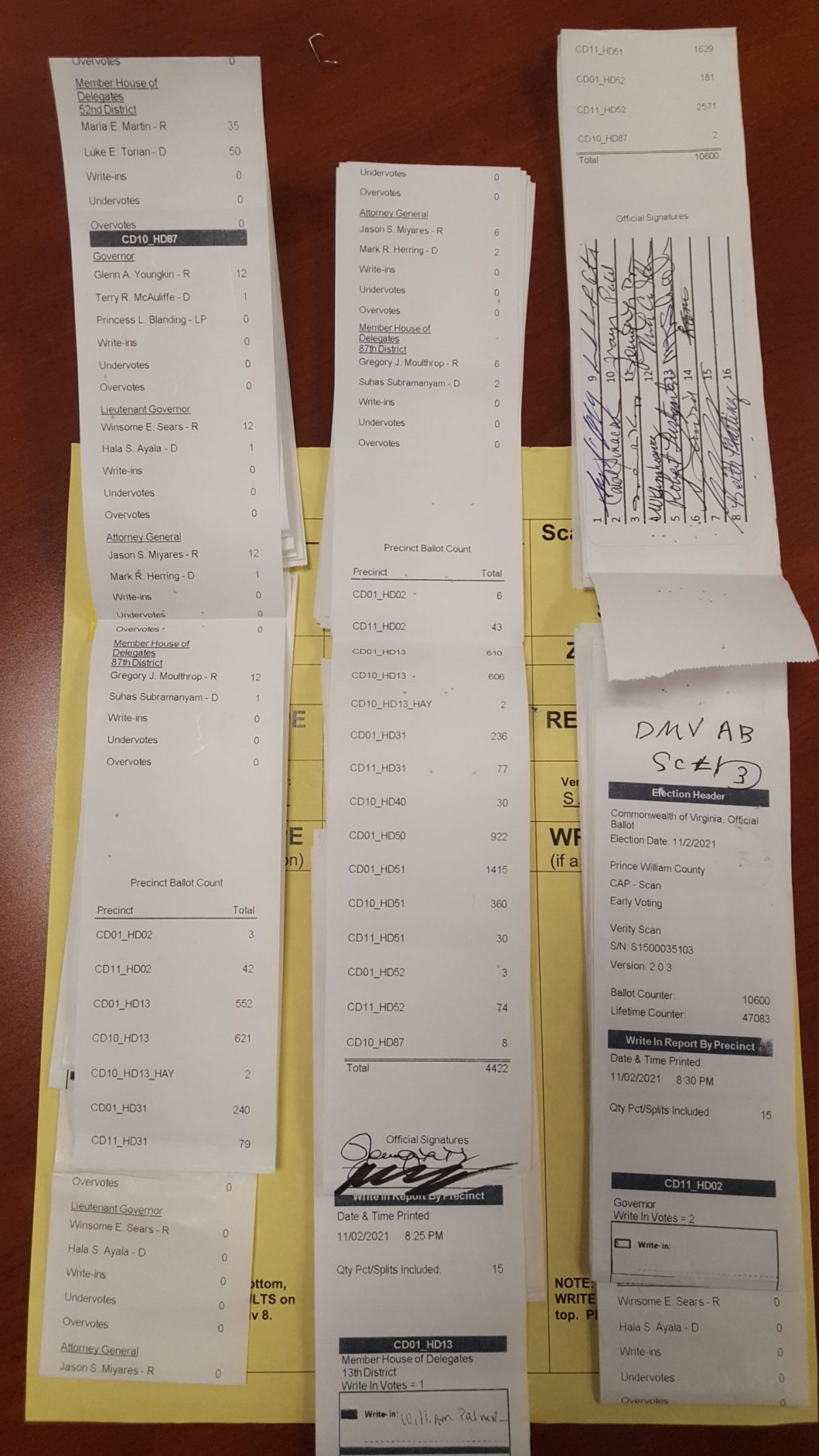
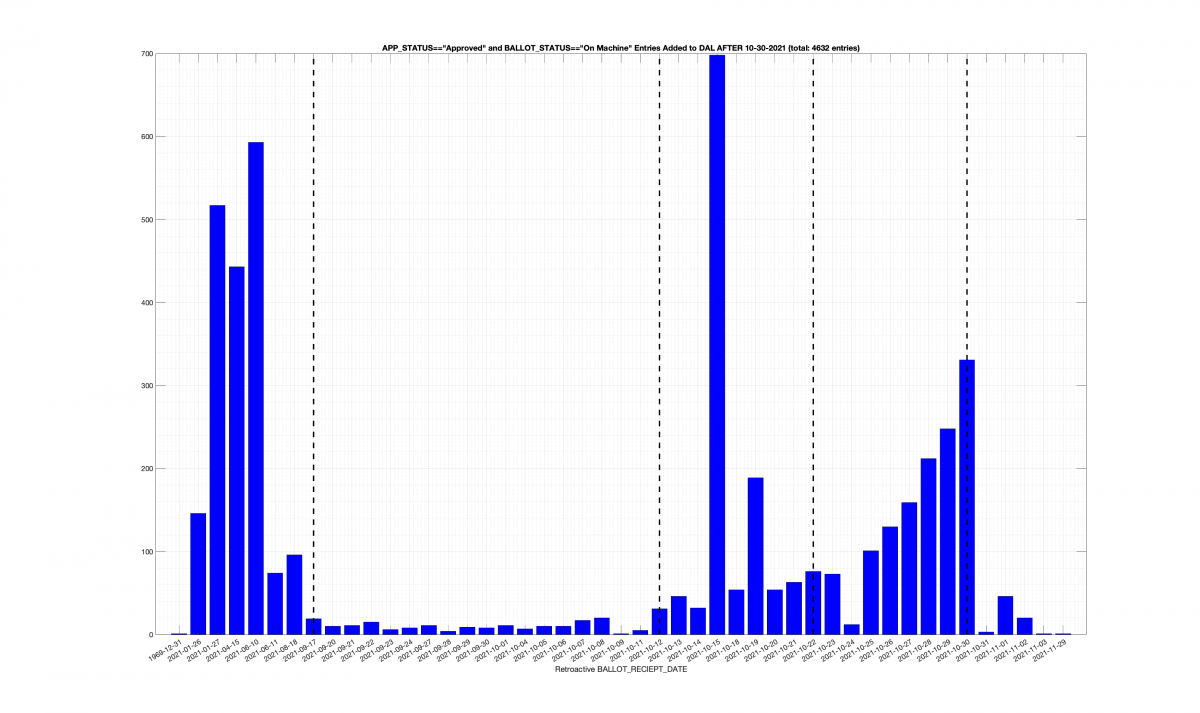
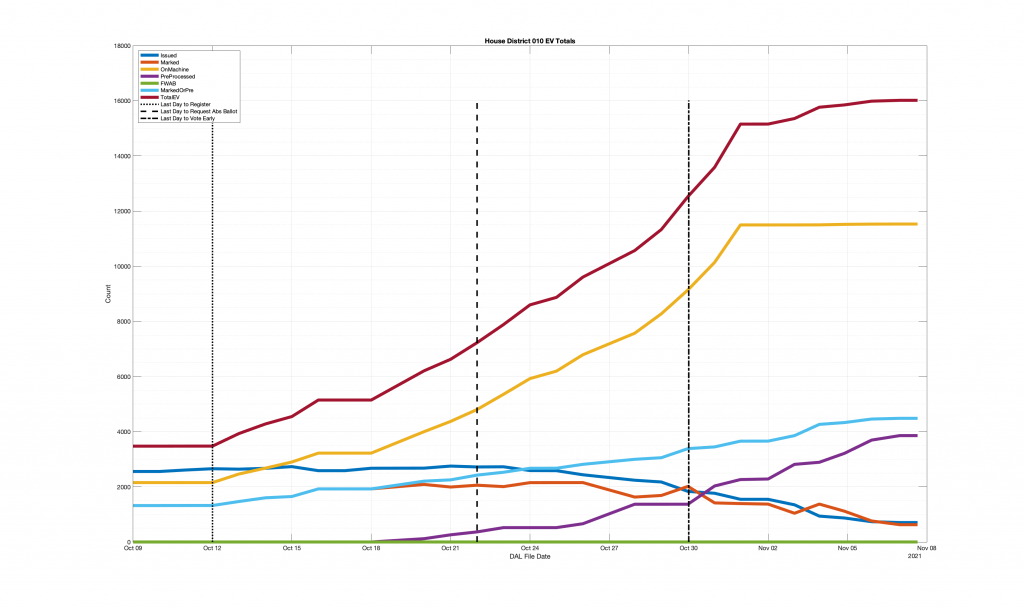
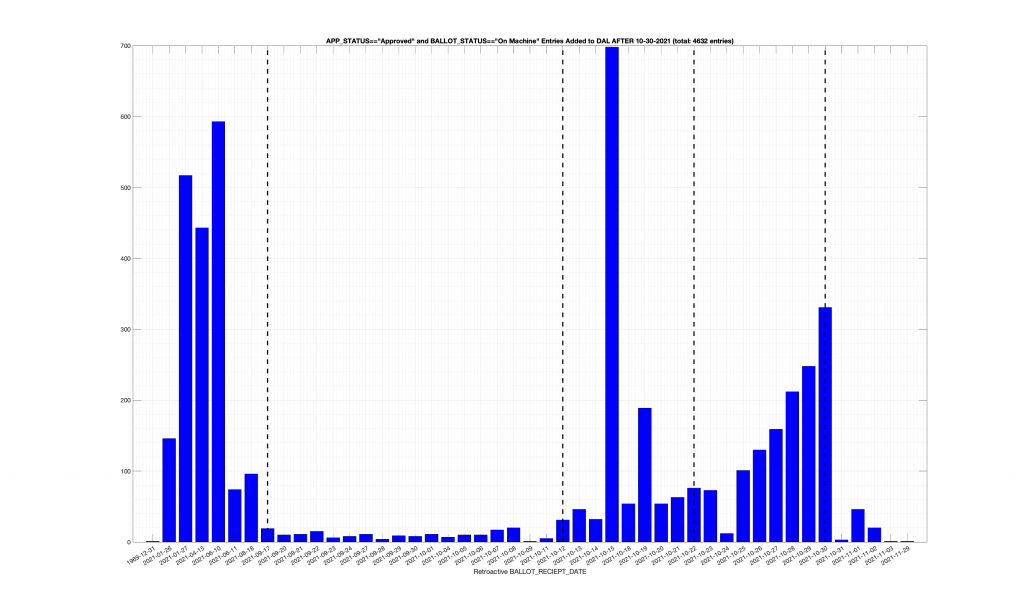
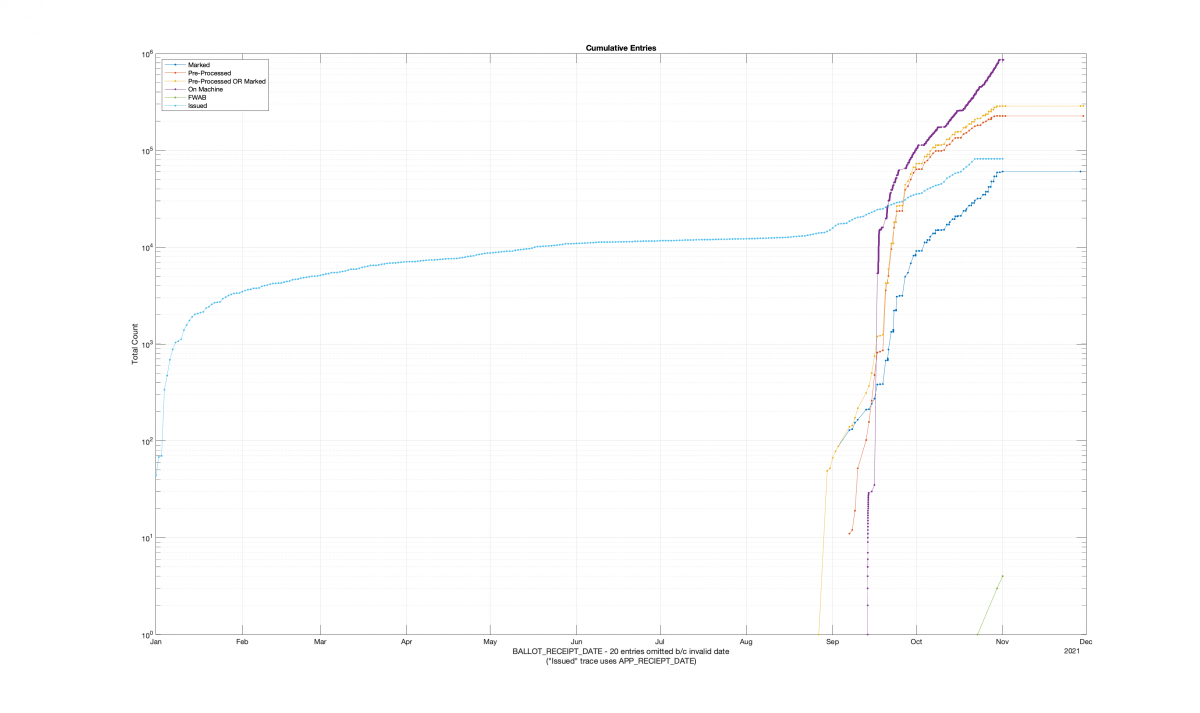
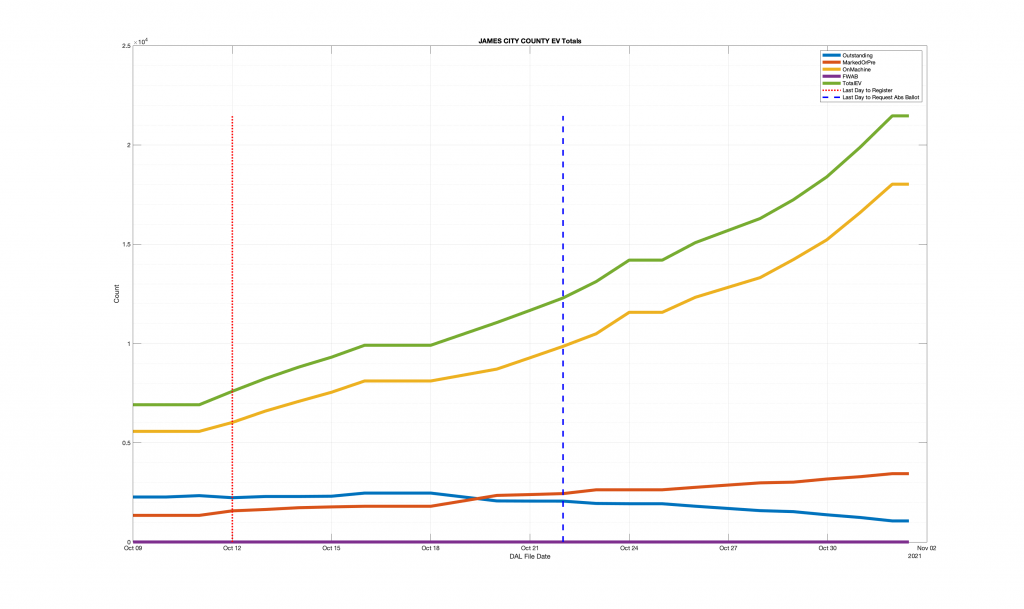
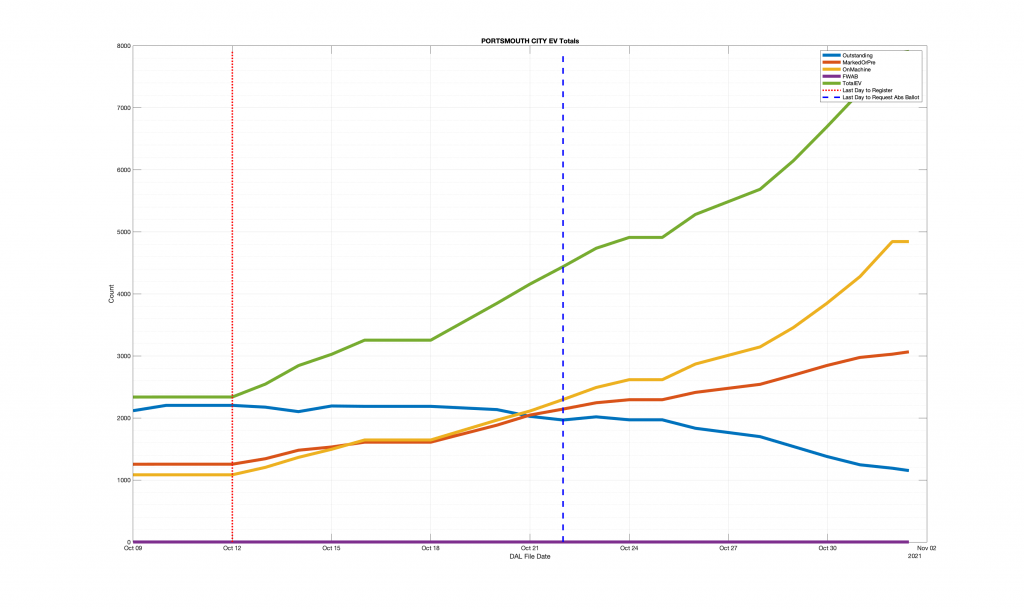
Locality + Precinct Name	Number Of Injected “On Machine” DAL Records
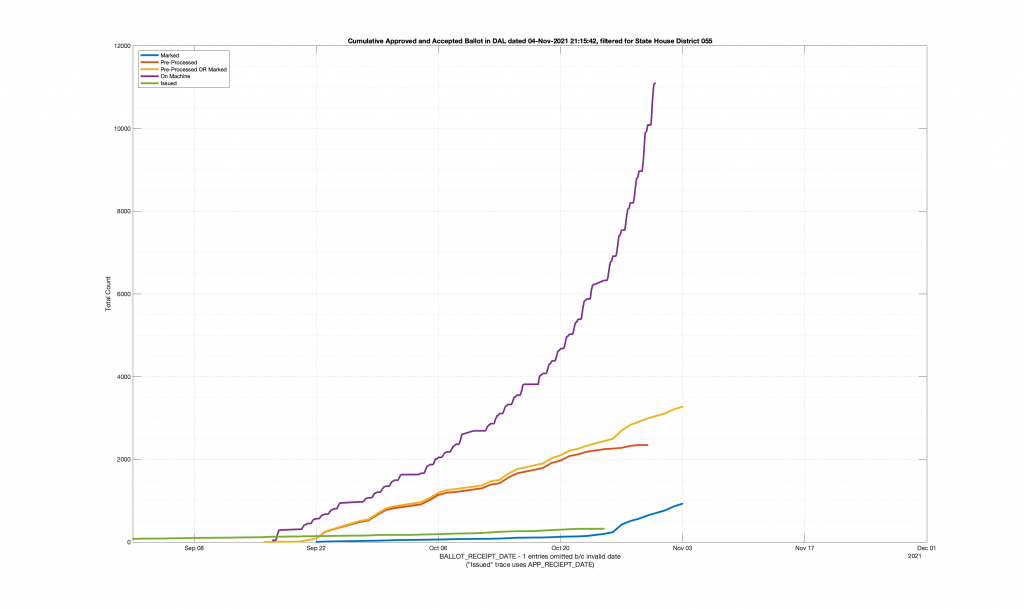
HANOVER COUNTY 704 – ELMONT 055	667
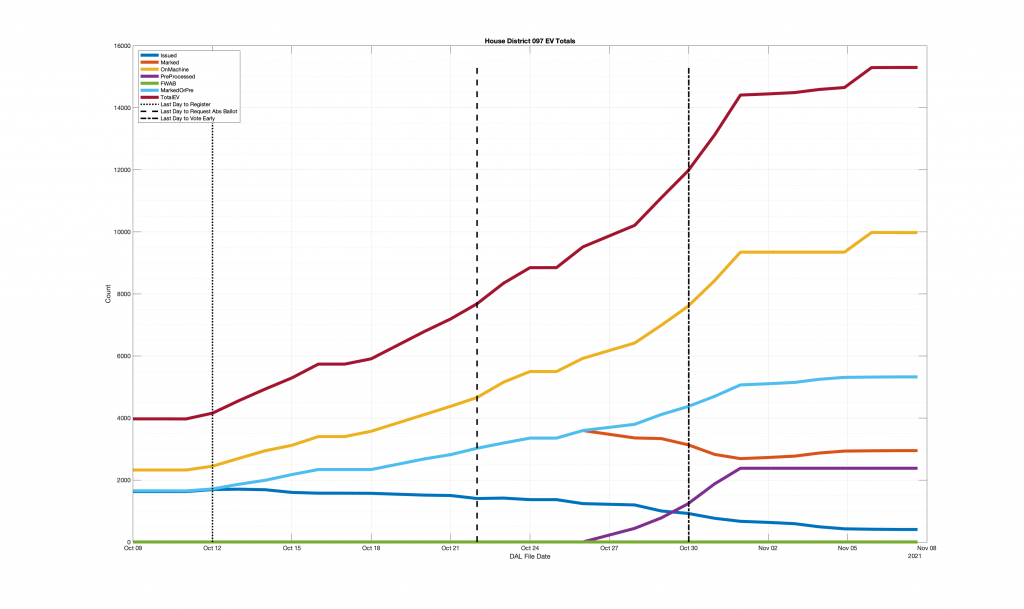
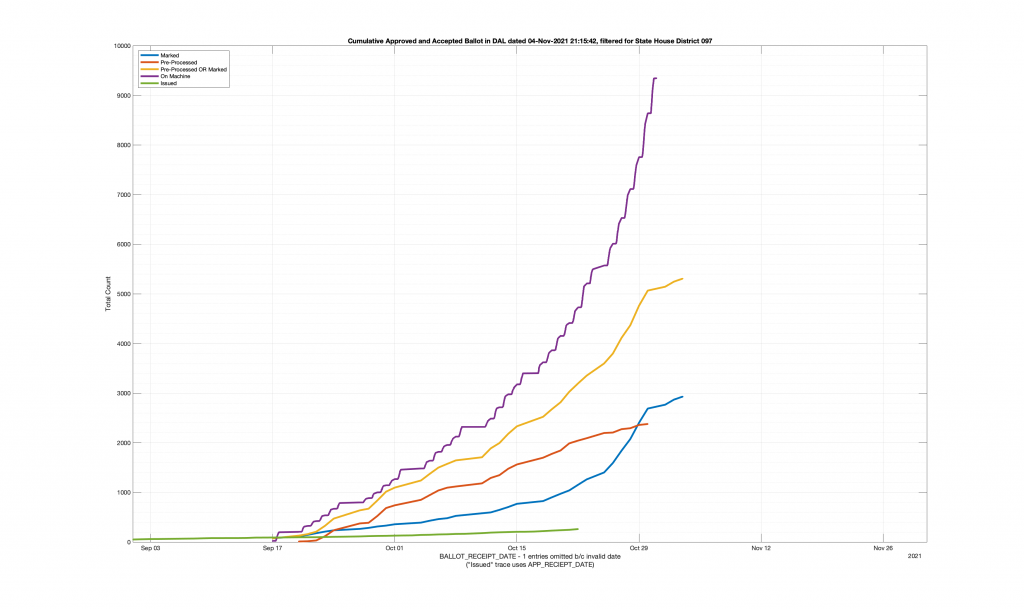
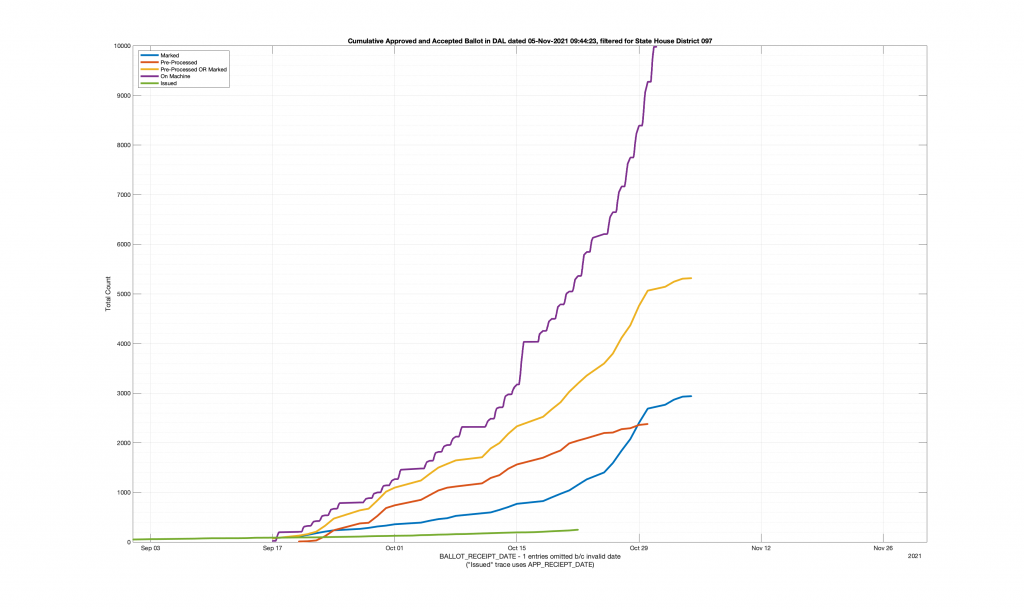
HANOVER COUNTY 602 – LEE DAVIS 097	635
LOUDOUN COUNTY 416 – HAMILTON 033	445
LOUDOUN COUNTY 214 – SUGARLAND NORTH 034	349
LOUDOUN COUNTY 708 – SENECA 034	320
LOUDOUN COUNTY 628 – MOOREFIELD STATION 032	99
LOUDOUN COUNTY 319 – JOHN CHAMPE 087	23
LOUDOUN COUNTY 313 – PINEBROOK 087	18
LOUDOUN COUNTY 112 – FREEDOM 087	17
TAZEWELL COUNTY 209 – JEFFERSONVILLE 003	14
GILES COUNTY 201 – PEARISBURG 012	13
SHENANDOAH COUNTY 401 – WOODSTOCK 015	13
KING GEORGE COUNTY 401 – SHILOH 099	12
LOUDOUN COUNTY 107 – LITTLE RIVER 067	12
LOUDOUN COUNTY 122 – HUTCHISON FARM 087	12
LOUDOUN COUNTY 126-GOSHEN POST 087	12
LOUDOUN COUNTY 316 – CREIGHTON’S CORNER 010	12
ARLINGTON COUNTY 010 – WILSON 048	11
ARLINGTON COUNTY 019 – ROSSLYN 048	11
KING GEORGE COUNTY 201 – MONROE 099	11
PULASKI COUNTY 401 – MASSIE 007	11
ARLINGTON COUNTY 018 – PARK LANE 047	10
NORTHAMPTON COUNTY 401 – PRECINCT 4-1 100	10
RUSSELL COUNTY 501 – WEST LEBANON 004	10
ARLINGTON COUNTY 041 – NAVY LEAGUE 047	9
NORTHAMPTON COUNTY 101 – PRECINCT 1-1 100	9
WASHINGTON COUNTY 302 – SOUTH ABINGDON 004	9
ARLINGTON COUNTY 009 – COLUMBIA 049	8
ARLINGTON COUNTY 048 – AUSA 047	8
CHESAPEAKE CITY 055 – GEORGETOWN EAST 077	8
FREDERICKSBURG CITY 401 – PRECINCT 1 – DISTRICT FOUR 028	8
KING GEORGE COUNTY 101 – COURTHOUSE 099	8
LOUDOUN COUNTY 114 – DULLES SOUTH 067	8
LOUDOUN COUNTY 408 – EVERGREEN 010	8
WILLIAMSBURG CITY 002 – MATOAKA 093	8
WINCHESTER CITY 101 – MERRIMANS 029	8
ARLINGTON COUNTY 004 – BALLSTON 047	7
ARLINGTON COUNTY 016 – LYON VILLAGE 048	7
ARLINGTON COUNTY 026 – FILLMORE 049	7
ARLINGTON COUNTY 040 – VIRGINIA SQUARE 047	7
BOTETOURT COUNTY 101 – DALEVILLE 019	7
BOTETOURT COUNTY 406 – FINCASTLE 019	7
CHESAPEAKE CITY 053 – FAIRWAYS 077	7
GLOUCESTER COUNTY 302 – ROANES 098	7
LOUDOUN COUNTY 121 – TOWN HALL 087	7
LOUDOUN COUNTY 318 – MADISON’S TRUST 010	7
LOUDOUN COUNTY 509 – TOLBERT 010	7
LOUDOUN COUNTY 623 – WELLER 032	7
MONTGOMERY COUNTY 202 – PRECINCT B-2 008	7
MONTGOMERY COUNTY 203 – PRECINCT B-3 007	7
PULASKI COUNTY 501 – ROBINSON 007	7
YORK COUNTY 401 – HARWOODS MILL 093	7
YORK COUNTY 402 – DARE 096	7
CHARLOTTESVILLE CITY 102 – CLARK 057	6
CHARLOTTESVILLE CITY 302 – JOHNSON 057	6
CHESAPEAKE CITY 008 – SOUTH NORFOLK RECREATION 077	6
CHESAPEAKE CITY 012 – GEORGETOWN 077	6
FREDERICKSBURG CITY 201 – PRECINCT 1 – DISTRICT TWO 028	6
GLOUCESTER COUNTY 401 – HAYES 098	6
LOUDOUN COUNTY 124 – LIBERTY 087	6
LOUDOUN COUNTY 320 – STONE HILL 087	6
LOUDOUN COUNTY 409 – CLARKES GAP 033	6
LOUDOUN COUNTY 817 – SANDERS CORNER 032	6
MATHEWS COUNTY 003 – PIANKATANK 098	6
NORFOLK CITY 211 – CHRYSLER MUSEUM 089	6
TAZEWELL COUNTY 301 – CEDAR BLUFF 003	6
TAZEWELL COUNTY 401 – RICHLANDS 003	6
WILLIAMSBURG CITY 001 – STRYKER 093	6
YORK COUNTY 201 – COVENTRY 093	6
ACCOMACK COUNTY 502 – RUE 100	5
ARLINGTON COUNTY 053 – MET PARK 049	5
CAMPBELL COUNTY 402 – COURT HOUSE 059	5
CAROLINE COUNTY 202 – SOUTH MADISON 055	5
CAROLINE COUNTY 501 – WEST MATTAPONI 055	5
CHESAPEAKE CITY 018 – INDIAN RIVER 077	5
COLONIAL HEIGHTS CITY 002 – SECOND 066	5
ESSEX COUNTY 101 – GREATER TAPPAHANNOCK 098	5
FREDERICKSBURG CITY 101 – PRECINCT 1 – DISTRICT ONE 088	5
LANCASTER COUNTY 401 – PRECINCT 4-1 099	5
LOUDOUN COUNTY 119 – ARCOLA 087	5
LOUDOUN COUNTY 322-BUFFALO TRAIL 087	5
LOUDOUN COUNTY 616 – EAGLE RIDGE 032	5
MANASSAS CITY 003 – METZ 050	5
MANASSAS CITY 005 – BALDWIN 050	5
MONTGOMERY COUNTY 701 – PRECINCT G-1 012	5
TAZEWELL COUNTY 501 – SPRINGVILLE 003	5
WASHINGTON COUNTY 101 – EAST ABINGDON 004	5
WASHINGTON COUNTY 301 – WATAUGA 005	5
WINCHESTER CITY 201 – VIRGINIA AVENUE 029	5
YORK COUNTY 302 – YORKTOWN 096	5
ARLINGTON COUNTY 008 – HUME 049	4
ARLINGTON COUNTY 017 – OVERLEE KNOLLS 047	4
ARLINGTON COUNTY 025 – ARLINGTON FOREST 047	4
ARLINGTON COUNTY 029 – DOMINION HILLS 047	4
ARLINGTON COUNTY 042 – SHIRLINGTON 045	4
ARLINGTON COUNTY 046 – CENTRAL 047	4
ARLINGTON COUNTY 054 – GARFIELD PARK 047	4
BOTETOURT COUNTY 201 – BLUE RIDGE 019	4
CHARLOTTESVILLE CITY 101 – Key Recreation 057	4
CHARLOTTESVILLE CITY 201 – CARVER 057	4
CHESAPEAKE CITY 029 – TANGLEWOOD 077	4
CHESAPEAKE CITY 042 – PARKWAYS 077	4
CHESAPEAKE CITY 059 – CLEARFIELD 078	4
CHESAPEAKE CITY 065 – WATERWAY II 021	4
CHESTERFIELD COUNTY 308 – SOUTH MANCHESTER 027	4
FREDERICKSBURG CITY 301 – PRECINCT 1 – DISTRICT THREE 088	4
FREDERICKSBURG CITY 402 – PRECINCT 2 – DISTRICT FOUR 088	4
GILES COUNTY 103 – NARROWS 012	4
GLOUCESTER COUNTY 101 – HARCUM 098	4
GLOUCESTER COUNTY 201 – COURTHOUSE 098	4
HENRICO COUNTY 106 – HERMITAGE 072	4
HENRICO COUNTY 303 – INNSBROOK 072	4
KING GEORGE COUNTY 301 – DAHLGREN 099	4
LANCASTER COUNTY 201 – PRECINCT 2-1 099	4
LOUDOUN COUNTY 123 – CARDINAL RIDGE 067	4
LOUDOUN COUNTY 308 – ST LOUIS 010	4
LOUDOUN COUNTY 420 – RIVER CREEK 010	4
LOUDOUN COUNTY 813 – SELDENS LANDING 032	4
MONTGOMERY COUNTY 101 – PRECINCT A-1 008	4
MONTGOMERY COUNTY 102 – PRECINCT A-2 012	4
MONTGOMERY COUNTY 204 – PRECINCT B-4 007	4
MONTGOMERY COUNTY 602 – PRECINCT F-2 012	4
ORANGE COUNTY 301 – THREE WEST 030	4
PRINCE GEORGE COUNTY 201 – BLAND 064	4
SHENANDOAH COUNTY 503 – TOMS BROOK 015	4
WINCHESTER CITY 402 – ROLLING HILLS 029	4
AMELIA COUNTY 301 – NUMBER THREE 061	3
APPOMATTOX COUNTY 202 – SPOUT SPRING 059	3
APPOMATTOX COUNTY 401 – COURTHOUSE 059	3
ARLINGTON COUNTY 007 – CHERRYDALE 048	3
ARLINGTON COUNTY 020 – THRIFTON 048	3
ARLINGTON COUNTY 023 – WESTOVER 047	3
ARLINGTON COUNTY 027 – JEFFERSON 049	3
ARLINGTON COUNTY 028 – WAKEFIELD 049	3
ARLINGTON COUNTY 035 – MADISON 048	3
ARLINGTON COUNTY 036 – MARSHALL 048	3
ARLINGTON COUNTY 039 – ASHLAWN 047	3
ARLINGTON COUNTY 044 – DAWSON TERRACE 048	3
ARLINGTON COUNTY 049 – MONROE 047	3
ARLINGTON COUNTY 050 – CRYSTAL PLAZA 048	3
BOTETOURT COUNTY 205 – ORCHARDS 017	3
BRISTOL CITY 002 – SECOND WARD 005	3
BRISTOL CITY 003 – THIRD WARD 005	3
CHARLOTTESVILLE CITY 202 – WALKER 057	3
CHARLOTTESVILLE CITY 301 – BENJAMIN TONSLER 057	3
CHARLOTTESVILLE CITY 303 – BUFORD 057	3
CHESAPEAKE CITY 005 – CRESTWOOD 077	3
CHESAPEAKE CITY 016 – HICKORY GROVE 078	3
CHESAPEAKE CITY 022 – NORFOLK HIGHLANDS 077	3
CHESAPEAKE CITY 056 – GREEN TREE 077	3
CHESAPEAKE CITY 057 – CYPRESS 077	3
CHESTERFIELD COUNTY 109 – ELIZABETH SCOTT 062	3
CUMBERLAND COUNTY 301 – PRECINCT 3 061	3
DINWIDDIE COUNTY 402 – MCKENNEY 063	3
FALLS CHURCH CITY 001 – FIRST WARD 053	3
FREDERICK COUNTY 101 – MERRIMANS 029	3
FREDERICK COUNTY 203 – REDLAND 029	3
GILES COUNTY 102 – RICH CREEK 012	3
GILES COUNTY 302 – PEMBROKE 012	3
GLOUCESTER COUNTY 301 – WHITE MARSH 098	3
GRAYSON COUNTY 203 – INDEPENDENCE 005	3
HARRISONBURG CITY 305 – MASSANETTA SPRINGS 025	3
HENRICO COUNTY 308 – RIVERS EDGE 056	3
HENRICO COUNTY 514 – ROLFE 070	3
HOPEWELL CITY 301 – WARD THREE 062	3
LANCASTER COUNTY 101 – PRECINCT 1-1 099	3
LOUDOUN COUNTY 108 – MERCER 087	3
LOUDOUN COUNTY 118 – MOOREFIELD 032	3
LOUDOUN COUNTY 120 – LUNSFORD 087	3
LOUDOUN COUNTY 201 – BERRYVILLE 033	3
LOUDOUN COUNTY 219 – GALILEE CHURCH 032	3
LOUDOUN COUNTY 321 – BRAMBLETON MIDDLE 010	3
LOUDOUN COUNTY 402 – WATERFORD 033	3
LOUDOUN COUNTY 502 – EAST LEESBURG 010	3
LOUDOUN COUNTY 505 – COOL SPRING 010	3
LOUDOUN COUNTY 506 – BRANDON PARK 010	3
LOUDOUN COUNTY 620 – RUSSELL BRANCH 032	3
LOUDOUN COUNTY 627 – ASHBROOK 032	3
LOUDOUN COUNTY 808 – STONE BRIDGE 032	3
LOUDOUN COUNTY 814 – NEWTON – LEE 032	3
MECKLENBURG COUNTY 903 – CLARKSVILLE 061	3
MONTGOMERY COUNTY 301 – PRECINCT C-1 008	3
MONTGOMERY COUNTY 304 – PRECINCT C-4 008	3
MONTGOMERY COUNTY 405 – PRECINCT D-5 007	3
MONTGOMERY COUNTY 501 – PRECINCT E-1 007	3
MONTGOMERY COUNTY 601 – PRECINCT F-1 012	3
NORTHAMPTON COUNTY 201 – PRECINCT 2-1 100	3
NORTHAMPTON COUNTY 501 – PRECINCT 5-1 100	3
NORTHUMBERLAND COUNTY 501 – 5A 099	3
PORTSMOUTH CITY 001 – EMANUEL A. M. E. CHURCH 080	3
PRINCE EDWARD COUNTY 101 – FARMVILLE 060	3
PRINCE EDWARD COUNTY 701 – WEST END 060	3
PULASKI COUNTY 102 – NEW RIVER 012	3
PULASKI COUNTY 103 – WEST CLOYD 007	3
ROANOKE COUNTY 507 – HUNTING HILLS 017	3
ROCKINGHAM COUNTY 202 – EDOM 026	3
ROCKINGHAM COUNTY 503 – MCGAHEYSVILLE 058	3
SHENANDOAH COUNTY 103 – NEW MARKET 015	3
SHENANDOAH COUNTY 302 – EDINBURG 015	3
SHENANDOAH COUNTY 303 – ST LUKE 015	3
SHENANDOAH COUNTY 601 – STRASBURG 015	3
SPOTSYLVANIA COUNTY 101 – PRECINCT 1 – DISTRICT ONE 088	3
SPOTSYLVANIA COUNTY 505 – BROCK 054	3
TAZEWELL COUNTY 103 – MUNDY TOWN 003	3
TAZEWELL COUNTY 303 – PAINT LICK 003	3
WARREN COUNTY 202 – LINDEN 018	3
WASHINGTON COUNTY 402 – MEADOWVIEW 005	3
WASHINGTON COUNTY 502 – DAMASCUS 005	3
WISE COUNTY 202 – WISE 001	3
WISE COUNTY 302 – EAST STONE GAP 001	3
YORK COUNTY 101 – QUEENS LAKE 096	3
YORK COUNTY 103 – MAGRUDER 096	3
YORK COUNTY 303 – EDGEHILL 093	3
YORK COUNTY 502 – BETHEL 091	3
ALBEMARLE COUNTY 101 – ZION 056	2
ALLEGHANY COUNTY 101 – ARRITT 019	2
ALLEGHANY COUNTY 701 – DISTRICT 2 019	2
AMELIA COUNTY 501 – NUMBER FIVE 061	2
AMHERST COUNTY 201 – COURT HOUSE 024	2
AMHERST COUNTY 501 – MADISON 023	2
APPOMATTOX COUNTY 102 – PAMPLIN 059	2
APPOMATTOX COUNTY 301 – US 460 059	2
ARLINGTON COUNTY 002 – ASHTON HEIGHTS 047	2
ARLINGTON COUNTY 006 – CRYSTAL CITY 048	2
ARLINGTON COUNTY 014 – CLARENDON 047	2
ARLINGTON COUNTY 015 – LYON PARK 047	2
ARLINGTON COUNTY 024 – WOODLAWN 048	2
ARLINGTON COUNTY 030 – GLEBE 049	2
ARLINGTON COUNTY 032 – OAKRIDGE 045	2
ARLINGTON COUNTY 034 – YORKTOWN 048	2
ARLINGTON COUNTY 038 – ARLINGTON VIEW 049	2
ARLINGTON COUNTY 045 – BUCKINGHAM 047	2
ARLINGTON COUNTY 047 – FOUR MILE RUN 049	2
AUGUSTA COUNTY 301 – FORT DEFIANCE 025	2
AUGUSTA COUNTY 501 – GREENVILLE 024	2
AUGUSTA COUNTY 801 – DOOMS 025	2
BATH COUNTY 201 – HOT SPRINGS 024	2
BOTETOURT COUNTY 301 – 3A 099	2
BOTETOURT COUNTY 302 – MILL CREEK 019	2
BRISTOL CITY 004 – FOURTH WARD 005	2
BRUNSWICK COUNTY 501 – TOTARO 075	2
BUCHANAN COUNTY 403 – SOUTH GRUNDY 003	2
BUCKINGHAM COUNTY 101 – PRECINCT 1 061	2
BUCKINGHAM COUNTY 302 – MT PLEASANT 060	2
CAMPBELL COUNTY 201 – WALKER 022	2
CAMPBELL COUNTY 601 – KINGS 022	2
CAMPBELL COUNTY 602 – CONCORD 059	2
CAROLINE COUNTY 102 – SPARTA 099	2
CAROLINE COUNTY 201 – NORTH MADISON 055	2
CAROLINE COUNTY 302 – WOODFORD 054	2
CARROLL COUNTY 105 – FANCY GAP 006	2
CARROLL COUNTY 201 – HILLSVILLE B 006	2
CHARLES CITY COUNTY 101 – PRECINCT 1-1 070	2
CHARLES CITY COUNTY 301 – PRECINCT 3-1 070	2
CHARLOTTE COUNTY 702 – BACON/SAXE 060	2
CHARLOTTESVILLE CITY 401 – VENABLE 057	2
CHESAPEAKE CITY 010 – OSCAR SMITH 077	2
CHESAPEAKE CITY 014 – GRASSFIELD 078	2
CHESAPEAKE CITY 015 – GREENBRIER MIDDLE SCHOOL 077	2
CHESAPEAKE CITY 023 – OAK GROVE 078	2
CHESAPEAKE CITY 024 – OAKLETTE 077	2
CHESAPEAKE CITY 031 – CARVER SCHOOL 077	2
CHESAPEAKE CITY 032 – PROVIDENCE 077	2
CHESAPEAKE CITY 034 – HICKORY MIDDLE SCHOOL 078	2
CHESAPEAKE CITY 043 – PLEASANT CROSSING 078	2
CHESAPEAKE CITY 201 – BARTLETT 064	2
CHESTERFIELD COUNTY 202 – SUTHERLAND 063	2
CHESTERFIELD COUNTY 204 – COURTS BLDG 064	2
CHESTERFIELD COUNTY 214 – LONGDALE 074	2
CHESTERFIELD COUNTY 304 – WINFREES STORE 063	2
CHESTERFIELD COUNTY 316 – SPRING RUN 027	2
CHESTERFIELD COUNTY 319 – MAGNOLIA 065	2
CHESTERFIELD COUNTY 404 – PROVIDENCE 027	2
CHESTERFIELD COUNTY 501 – FIFTH WARD FIRST PRECINCT 063	2
CHESTERFIELD COUNTY 518 – WHITLOCKS 070	2
CLARKE COUNTY 401 – MINERAL 056	2
COLONIAL HEIGHTS CITY 001 – FIRST 066	2
COLONIAL HEIGHTS CITY 004 – FOURTH 066	2
COLONIAL HEIGHTS CITY 101 – WARD ONE 062	2
DINWIDDIE COUNTY 202 – SUTHERLAND 063	2
DINWIDDIE COUNTY 303 – LITTLE ZION 063	2
EMPORIA CITY 601 – DISTRICT 6 075	2
ESSEX COUNTY 201 – NORTH 098	2
FAIRFAX CITY 040 – VIRGINIA SQUARE 047	2
FAIRFAX COUNTY 318 – WESTMORELAND 048	2
FAIRFAX COUNTY 501 – BAILEYS #1 038	2
FAIRFAX COUNTY 502 – BENTONVILLE 015	2
FALLS CHURCH CITY 003 – THIRD WARD 053	2
FAUQUIER COUNTY 101 – ZION 056	2
FAUQUIER COUNTY 404 – SPRINGS VALLEY 018	2
FAUQUIER COUNTY 501 – THE PLAINS 018	2
FLUVANNA COUNTY 101 – PALMYRA 058	2
FRANKLIN COUNTY 415 – SKIPWITH 073	2
FREDERICK COUNTY 401 – CARPERS VALLEY 010	2
FREDERICK COUNTY 503 – CANTERBURG 029	2
FREDERICK COUNTY 603 – GREENWOOD 033	2
GILES COUNTY 301 – EGGLESTON 012	2
GILES COUNTY 303 – NEWPORT 012	2
GLOUCESTER COUNTY 202 – BOTETOURT 098	2
GLOUCESTER COUNTY 402 – SARAHS CREEK 098	2
GLOUCESTER COUNTY 501 – ACHILLES 098	2
GOOCHLAND COUNTY 202 – SANDY HOOK 065	2
GOOCHLAND COUNTY 402 – CENTERVILLE 056	2
GREENE COUNTY 201 – RUCKERSVILLE 058	2
GREENSVILLE COUNTY 202 – PRECINCT 2-B 075	2
GREENSVILLE COUNTY 402 – PRECINCT 4-B 075	2
HALIFAX COUNTY 403 – CENTER 060	2
HALIFAX COUNTY 801 – SOUTH BOSTON 060	2
HAMPTON CITY 103 – MAGRUDER 096	2
HAMPTON CITY 211 – PALMER 095	2
HANOVER COUNTY 408 – LAUDERDALE 072	2
HENRICO COUNTY 102 – DUMBARTON 072	2
HENRICO COUNTY 105 – GREENDALE 072	2
HENRICO COUNTY 110 – JOHNSON 073	2
HENRICO COUNTY 215 – MAPLEWOOD 074	2
HENRICO COUNTY 216 – MOODY 074	2
HENRICO COUNTY 301 – CAUSEWAY 056	2
HENRICO COUNTY 302 – CEDARFIELD 073	2
HENRICO COUNTY 304 – JACKSON DAVIS 073	2
HENRICO COUNTY 402 – CENTERVILLE 056	2
HENRICO COUNTY 504 – DONAHOE 074	2
HENRICO COUNTY 506 – EANES 070	2
HENRICO COUNTY 508 – HIGHLAND SPRINGS 074	2
HENRICO COUNTY 516 – SULLIVANS 070	2
HENRY COUNTY 505 – DYERS STORE 016	2
HOPEWELL CITY 401 – WARD FOUR 062	2
ISLE OF WIGHT COUNTY 101 – SMITHFIELD 064	2
ISLE OF WIGHT COUNTY 302 – PONS 064	2
JAMES CITY COUNTY 403 – STONEHOUSE C 096	2
KING WILLIAM COUNTY 101 – HARTWOOD 088	2
KING WILLIAM COUNTY 202 – COURTHOUSE 097	2
LOUDOUN COUNTY 117 – CARTER 087	2
LOUDOUN COUNTY 207 – RIVER BEND 034	2
LOUDOUN COUNTY 208 – ALGONKIAN 032	2
LOUDOUN COUNTY 217 – SOUTH BANK 034	2
LOUDOUN COUNTY 218 – UNIVERSITY CENTER 032	2
LOUDOUN COUNTY 301 – PURCELLVILLE 033	2
LOUDOUN COUNTY 302 – ROUND HILL 033	2
LOUDOUN COUNTY 309 – ALDIE 010	2
LOUDOUN COUNTY 310 – MOUNTAIN VIEW 033	2
LOUDOUN COUNTY 311 – ROUND HILL ELEMENTARY 033	2
LOUDOUN COUNTY 422 – SYCOLIN CREEK 010	2
LOUDOUN COUNTY 501 – WEST LEESBURG 010	2
LOUDOUN COUNTY 504 – SMARTS MILL 010	2
LOUDOUN COUNTY 617 – OAK GROVE 087	2
LOUDOUN COUNTY 619 – RIDGETOP 087	2
LOUDOUN COUNTY 621 – DOMINION TRAIL 032	2
LOUDOUN COUNTY 629 – DISCOVERY 087	2
LOUDOUN COUNTY 815 – BELMONT RIDGE 032	2
LOUDOUN COUNTY 819 – HERITAGE CHURCH 032	2
LOUISA COUNTY 301 – PATRICK HENRY NO 1 056	2
LOUISA COUNTY 401 – MINERAL 056	2
LYNCHBURG CITY 404 – FOURTH WARD FOURTH PRECINCT 023	2
MANASSAS CITY 001 – DEAN 050	2
MANASSAS CITY 006 – ROUND 050	2
MECKLENBURG COUNTY 202 – BLUESTONE SENIOR HIGH SCHOOL 061	2
MECKLENBURG COUNTY 501 – SOUTH HILL 061	2
MONTGOMERY COUNTY 103 – PRECINCT A-3 012	2
MONTGOMERY COUNTY 201 – LITTLE RIVER 007	2
MONTGOMERY COUNTY 403 – PRECINCT D-3 007	2
MONTGOMERY COUNTY 502 – PRECINCT E-2 012	2
MONTGOMERY COUNTY 702 – PRECINCT G-2 012	2
NELSON COUNTY 301 – SHIPMAN 059	2
NEWPORT NEWS CITY 102 – STONEY RUN 094	2
NEWPORT NEWS CITY 104 – MCINTOSH 094	2
NEWPORT NEWS CITY 205 – DEEP CREEK 094	2
NEWPORT NEWS CITY 219 – DEER PARK 095	2
NEWPORT NEWS CITY 304 – CHESTNUT 095	2
NEWPORT NEWS CITY 315 – SEDGEFIELD 095	2
NEWPORT NEWS CITY 320 – WATKINS 095	2
NORFOLK CITY 306 – LINDENWOOD 089	2
NORFOLK CITY 507 – PRETLOW 100	2
NORTHAMPTON COUNTY 301 – PRECINCT 3-1 100	2
NORTHAMPTON COUNTY 307 – CROSSROADS 025	2
NORTHUMBERLAND COUNTY 101 – 1A 099	2
ORANGE COUNTY 101 – ONE WEST 030	2
ORANGE COUNTY 102 – ONE EAST 030	2
ORANGE COUNTY 202 – TWO EAST 030	2
PORTSMOUTH CITY 031 – WEST PARK CHURCH OF CHRIST 080	2
POWHATAN COUNTY 101 – VERA 059	2
PRINCE EDWARD COUNTY 302 – MT PLEASANT 060	2
PRINCE EDWARD COUNTY 302 – PRECINCT 3-2 061	2
PRINCE GEORGE COUNTY 102 – TEMPLETON 064	2
PRINCE GEORGE COUNTY 204 – COURTS BLDG 064	2
PRINCE WILLIAM COUNTY 203 – RUBY 002	2
PRINCE WILLIAM COUNTY 409 – TYLER 013	2
PRINCE WILLIAM COUNTY 513 – LYNNWOOD 051	2
PRINCE WILLIAM COUNTY 712 – LEESYLVANIA 002	2
PULASKI COUNTY 202 – SOUTH PULASKI 007	2
PULASKI COUNTY 301 – DUBLIN 007	2
RICHMOND CITY 402 – CRESTVIEW 073	2
ROANOKE COUNTY 202 – BURLINGTON 017	2
ROANOKE COUNTY 205 – ORCHARDS 017	2
ROANOKE COUNTY 503 – CAVE SPRING 008	2
ROANOKE COUNTY 504 – OGDEN 017	2
ROANOKE COUNTY 506 – MOUNT VERNON 017	2
ROCKBRIDGE COUNTY 101 – AIRPORT 024	2
ROCKBRIDGE COUNTY 402 – MOUNTAIN VIEW 024	2
ROCKINGHAM COUNTY 204 – MT CLINTON 026	2
ROCKINGHAM COUNTY 303 – MELROSE 026	2
ROCKINGHAM COUNTY 307 – CROSSROADS 025	2
ROCKINGHAM COUNTY 502 – SWIFT RUN 058	2
RUSSELL COUNTY 304 – CLEVELAND 004	2
RUSSELL COUNTY 602 – ELK GARDEN 004	2
SHENANDOAH COUNTY 201 – CONICVILLE 015	2
SHENANDOAH COUNTY 202 – MT JACKSON 015	2
STAFFORD COUNTY 302 – WIDEWATER 002	2
STAFFORD COUNTY 402 – COURTHOUSE 028	2
STAFFORD COUNTY 502 – FLINT HILL 018	2
SUFFOLK CITY 504 – LAKE COHOON 076	2
SUFFOLK CITY 602 – OLDE TOWNE 076	2
TAZEWELL COUNTY 102 – TIP TOP 003	2
TAZEWELL COUNTY 104 – FALLS MILLS 003	2
TAZEWELL COUNTY 502 – GRAHAM 003	2
VIRGINIA BEACH CITY 010 – GREAT NECK 082	2
VIRGINIA BEACH CITY 502 – BETHEL 091	2
WARREN COUNTY 501 – SOUTH RIVER 018	2
WARREN COUNTY 504 – BROWNTOWN 015	2
WARREN COUNTY 601 – STRASBURG 015	2
WASHINGTON COUNTY 603 – VALLEY INSTITUTE 004	2
WASHINGTON COUNTY 701 – HIGH POINT 005	2
WAYNESBORO CITY 603 – LYNDHURST 020	2
WINCHESTER CITY 102 – OLD TOWN 029	2
WINCHESTER CITY 103 – KERNSTOWN 029	2
WISE COUNTY 401 – CLINCH VALLEY 001	2
WYTHE COUNTY 401 – FRIES 005	2
YORK COUNTY 301 – SEAFORD 096	2
YORK COUNTY 303 – EDGEHILL 096	2
YORK COUNTY 403 – GRAFTON 096	2
YORK COUNTY 501 – TABB 093	2
ACCOMACK COUNTY 301 – NEW CHURCH 100	1
ACCOMACK COUNTY 701 – NANDUA 100	1
ACCOMACK COUNTY 802 – MELFA 100	1
ACCOMACK COUNTY 901 – PAINTER 100	1
ALBEMARLE COUNTY 101 – Key Recreation 057	1
ALBEMARLE COUNTY 101 – ROCKFISH 020	1
ALBEMARLE COUNTY 102 – CLARK 057	1
ALBEMARLE COUNTY 301 – BENJAMIN TONSLER 057	1
ALBEMARLE COUNTY 401 – MIDWAY 058	1
ALBEMARLE COUNTY 502 – BETHEL 091	1
ALBEMARLE COUNTY 502 – NELLYSFORD 020	1
ALEXANDRIA CITY 101 – HARTWOOD 088	1
ALEXANDRIA CITY 102 – CITY HALL 045	1
ALEXANDRIA CITY 110 – CHARLES HOUSTON CENTER 045	1
ALEXANDRIA CITY 201 – NAOMI L. BROOKS SCHOOL 045	1
ALEXANDRIA CITY 304 – SAMUEL TUCKER SCHOOL 046	1
ALEXANDRIA CITY 318 – MADISON’S TRUST 010	1
ALEXANDRIA CITY 616 – EAGLE RIDGE 032	1
AMELIA COUNTY 301 – BENJAMIN TONSLER 057	1
AMELIA COUNTY 401 – NUMBER FOUR 061	1
AMHERST COUNTY 102 – NEW GLASGOW 024	1
APPOMATTOX COUNTY 501 – DARLINGTON HTS 060	1
APPOMATTOX COUNTY 501 – OAKVILLE 059	1
ARLINGTON COUNTY 001 – ARLINGTON 049	1
ARLINGTON COUNTY 003 – AURORA HILLS 045	1
ARLINGTON COUNTY 005 – BARCROFT 047	1
ARLINGTON COUNTY 011 – EAST FALLS CHURCH 047	1
ARLINGTON COUNTY 012 – FAIRLINGTON 045	1
ARLINGTON COUNTY 013 – GLEN CARLYN 047	1
ARLINGTON COUNTY 022 – ABINGDON 045	1
ARLINGTON COUNTY 031 – LEXINGTON 047	1
ARLINGTON COUNTY 033 – ROCK SPRING 048	1
ARLINGTON COUNTY 043 – CAMPBELL 049	1
ARLINGTON COUNTY 101 – ZION 056	1
ARLINGTON COUNTY 301 – THREE WEST 030	1
ARLINGTON COUNTY 401 – THREE FORKS 059	1
ARLINGTON COUNTY 407 – HARPER PARK 010	1
AUGUSTA COUNTY 103 – VERONA 025	1
AUGUSTA COUNTY 503 – SPOTTSWOOD 024	1
AUGUSTA COUNTY 504 – WHITE HILL 024	1
AUGUSTA COUNTY 601 – SHERANDO 020	1
AUGUSTA COUNTY 602 – RIDGEVIEW 024	1
AUGUSTA COUNTY 603 – LYNDHURST 020	1
BATH COUNTY 101 – WARM SPRINGS 024	1
BATH COUNTY 501 – HEALING SPRINGS 024	1
BEDFORD COUNTY 101 – BROOKVILLE 022	1
BEDFORD COUNTY 205 – SAUNDERS VOL FIRE CO 022	1
BEDFORD COUNTY 502 – WASSONA 006	1
BEDFORD COUNTY 701 – GOODE VOL RESCUE SQUAD 019	1
BEDFORD COUNTY 703 – THAXTON BAPTIST CHURCH #2 023	1
BLAND COUNTY 301 – HOLLYBROOK 003	1
BOTETOURT COUNTY 301 – BUCHANAN 019	1
BOTETOURT COUNTY 403 – EAGLE ROCK 019	1
BOTETOURT COUNTY 403 – NORTH VINTON 017	1
BOTETOURT COUNTY 404 – SOUTH VINTON 017	1
BOTETOURT COUNTY 505 – CLEARBROOK 017	1
BRISTOL CITY 001 – FIRST WARD 005	1
BRUNSWICK COUNTY 402 – KING’S STORE 075	1
BUCHANAN COUNTY 301 – SLATE 003	1
BUCHANAN COUNTY 302 – NORTH GRUNDY 003	1
CAMPBELL COUNTY 102 – NEW LONDON 022	1
CAMPBELL COUNTY 201 – LOVINGSTON 059	1
CAMPBELL COUNTY 401 – FOURTH WARD FIRST PRECINCT 023	1
CAMPBELL COUNTY 501 – MADISON 023	1
CAMPBELL COUNTY 501 – SPRING HILL 022	1
CAMPBELL COUNTY 502 – YELLOW BRANCH 059	1
CAROLINE COUNTY 101 – BOWLING GREEN 099	1
CAROLINE COUNTY 401 – DAWN 055	1
CAROLINE COUNTY 401 – SHILOH 099	1
CAROLINE COUNTY 502 – MILFORD 055	1
CAROLINE COUNTY 602 – LAKE 055	1
CARROLL COUNTY 202 – PRECINCT B-2 008	1
CARROLL COUNTY 202 – WISE 001	1
CARROLL COUNTY 501 – VAUGHAN 006	1
CARROLL COUNTY 502 – GLADEVILLE 006	1
CHARLES CITY COUNTY 201 – PRECINCT 2-1 070	1
CHARLOTTE COUNTY 201 – RED OAK WYLLIESBURG 060	1
CHARLOTTE COUNTY 702 – SOUTH ANNA 056	1
CHARLOTTESVILLE CITY 314 – THREE CHOPT 073	1
CHARLOTTESVILLE CITY 402 – ALUMNI HALL 057	1
CHESAPEAKE CITY 006 – DEEP CREEK 081	1
CHESAPEAKE CITY 009 – BELLS MILL 078	1
CHESAPEAKE CITY 011 – GENEVA PARK 081	1
CHESAPEAKE CITY 020 – E W CHITTUM 081	1
CHESAPEAKE CITY 027 – CAVALIER MANOR RECREATION CENTER 080	1
CHESAPEAKE CITY 033 – WESTOVER 077	1
CHESAPEAKE CITY 046 – BELLS MILL II 078	1
CHESAPEAKE CITY 048 – JOLLIFF MIDDLE SCHOOL 081	1
CHESAPEAKE CITY 049 – WATERWAY 021	1
CHESAPEAKE CITY 050 – RIVER WALK 077	1
CHESAPEAKE CITY 051 – COOPERS WAY 078	1
CHESAPEAKE CITY 062 – FENTRESS 078	1
CHESAPEAKE CITY 063 – POPLAR BRANCH 078	1
CHESAPEAKE CITY 064 – DEEP CREEK II 081	1
CHESAPEAKE CITY 121 – TOWN HALL 087	1
CHESAPEAKE CITY 218 – WILLARD 089	1
CHESTERFIELD COUNTY 001 – FIRST 066	1
CHESTERFIELD COUNTY 101 – PRECINCT 1 061	1
CHESTERFIELD COUNTY 102 – IVOR 075	1
CHESTERFIELD COUNTY 103 – ENON 062	1
CHESTERFIELD COUNTY 108 – ECOFF 062	1
CHESTERFIELD COUNTY 202 – GRACELAND 065	1
CHESTERFIELD COUNTY 206 – BELMONT 066	1
CHESTERFIELD COUNTY 209 – SALEM CHURCH 062	1
CHESTERFIELD COUNTY 210 – FIVE FORKS 066	1
CHESTERFIELD COUNTY 301 – ETTRICK 066	1
CHESTERFIELD COUNTY 301 – NUMBER THREE 061	1
CHESTERFIELD COUNTY 303 – MATOACA 066	1
CHESTERFIELD COUNTY 310 – TOMAHAWK 065	1
CHESTERFIELD COUNTY 313 – WOOLRIDGE 065	1
CHESTERFIELD COUNTY 314 – LONGHOUSE 066	1
CHESTERFIELD COUNTY 315 – BAILEY BRIDGE 027	1
CHESTERFIELD COUNTY 316 – COLONIAL TRAIL 056	1
CHESTERFIELD COUNTY 317 – BIRKDALE 063	1
CHESTERFIELD COUNTY 401 – HAMPDEN 060	1
CHESTERFIELD COUNTY 405 – LA PRADE 027	1
CHESTERFIELD COUNTY 407 – MONACAN 027	1
CHESTERFIELD COUNTY 410 – WAGSTAFF 027	1
CHESTERFIELD COUNTY 413 – RIDGEFIELD 072	1
CHESTERFIELD COUNTY 415 – EVERGREEN 027	1
CHESTERFIELD COUNTY 416 – EVERGREEN WEST 065	1
CHESTERFIELD COUNTY 417 – EDGEWATER 065	1
CHESTERFIELD COUNTY 503 – CHICKAHOMINY 074	1
CHESTERFIELD COUNTY 504 – ROBIOUS 068	1
CHESTERFIELD COUNTY 505 – DOREY 070	1
CHESTERFIELD COUNTY 510 – SYCAMORE 068	1
CHESTERFIELD COUNTY 513 – BEAUFONT 027	1
CHESTERFIELD COUNTY 601 – CHILESBURG 055	1
CHESTERFIELD COUNTY 603 – WHITE OAK 028	1
CHESTERFIELD COUNTY 903 – CLARKSVILLE 061	1
CLARKE COUNTY 301 – MILLWOOD 010	1
CLARKE COUNTY 401 – WHITE POST 010	1
CLARKE COUNTY 501 – PRECINCT E-1 007	1
COLONIAL HEIGHTS CITY 005 – FIFTH 066	1
COLONIAL HEIGHTS CITY 102 – RICH CREEK 012	1
COVINGTON CITY 401 – PRECINCT 4-1 019	1
CULPEPER COUNTY 201 – TWO WEST 030	1
CULPEPER COUNTY 303 – CARDOVA 030	1
CUMBERLAND COUNTY 501 – PRECINCT 5 061	1
DANVILLE CITY 103 – TWIN SPRINGS 016	1
DANVILLE CITY 405 – RINGGOLD 014	1
DICKENSON COUNTY 101 – SOUTH CLINTWOOD 004	1
DICKENSON COUNTY 104 – WEST POUND 004	1
DICKENSON COUNTY 303 – RIDGE 004	1
DINWIDDIE COUNTY 502 – CHESDIN 063	1
EMPORIA CITY 201 – PRECINCT 2-1 075	1
EMPORIA CITY 302 – PRECINCT 3-A 075	1
EMPORIA CITY 401 – PRECINCT 4-1 075	1
ESSEX COUNTY 301 – SOUTH 098	1
ESSEX COUNTY 401 – CENTRAL 098	1
FAIRFAX CITY 001 – ONE 037	1
FAIRFAX COUNTY 046 – CENTRAL 047	1
FAIRFAX COUNTY 101 – ZION 056	1
FAIRFAX COUNTY 102 – OLD TOWN 029	1
FAIRFAX COUNTY 113 – CANTERBURY 039	1
FAIRFAX COUNTY 126-GOSHEN POST 087	1
FAIRFAX COUNTY 132 – MONUMENT 037	1
FAIRFAX COUNTY 201 – AMISSVILLE 018	1
FAIRFAX COUNTY 201 – ROCK HILL 002	1
FAIRFAX COUNTY 202 – TWO EAST 030	1
FAIRFAX COUNTY 208 – RESTON #1 036	1
FAIRFAX COUNTY 209 – RESTON #2 036	1
FAIRFAX COUNTY 219 – WESTBRIAR 034	1
FAIRFAX COUNTY 302 – JOHNSON 057	1
FAIRFAX COUNTY 310 – KIRBY 048	1
FAIRFAX COUNTY 311 – ROUND HILL ELEMENTARY 033	1
FAIRFAX COUNTY 319 – JOHN CHAMPE 087	1
FAIRFAX COUNTY 328 – HICKORY 034	1
FAIRFAX COUNTY 401 – 4A 099	1
FAIRFAX COUNTY 401 – WOODSTOCK 015	1
FAIRFAX COUNTY 403 – BROOKE 028	1
FAIRFAX COUNTY 404 – FRANCONIA 043	1
FAIRFAX COUNTY 410 – ROSE HILL 043	1
FAIRFAX COUNTY 421 – KINGSTOWNE 043	1
FAIRFAX COUNTY 502 – BETHEL 091	1
FAIRFAX COUNTY 502 – FIVE NORTH 030	1
FAIRFAX COUNTY 622 – FARMWELL STATION 032	1
FAIRFAX COUNTY 627 – ASHBROOK 032	1
FAIRFAX COUNTY 701 – WOODLANDS 088	1
FAIRFAX COUNTY 721 – MERRIFIELD 053	1
FAIRFAX COUNTY 804 – COLCHESTER 040	1
FAIRFAX COUNTY 918 – CENTREVILLE 040	1
FALLS CHURCH CITY 002 – SECOND WARD 053	1
FALLS CHURCH CITY 401 – VENABLE 057	1
FAUQUIER COUNTY 026 – FILLMORE 049	1
FAUQUIER COUNTY 101 – KETTLE RUN 031	1
FAUQUIER COUNTY 102 – PASSAPATANZY 099	1
FAUQUIER COUNTY 104 – LOIS 088	1
FAUQUIER COUNTY 202 – AIRLIE 018	1
FAUQUIER COUNTY 203 – WARRENTON 018	1
FAUQUIER COUNTY 303 – BEALETON 018	1
FAUQUIER COUNTY 401 – WOODSTOCK 015	1
FAUQUIER COUNTY 402 – LEEDS 018	1
FAUQUIER COUNTY 403 – WATERLOO 018	1
FAUQUIER COUNTY 503 – BROAD RUN 018	1
FLOYD COUNTY 203 – PRECINCT B-3 007	1
FLOYD COUNTY 301 – COURTHOUSE 007	1
FLUVANNA COUNTY 101 – FIRST WARD FIRST PRECINCT 023	1
FLUVANNA COUNTY 202 – LOUISA #2 056	1
FLUVANNA COUNTY 301 – PATRICK HENRY NO 1 056	1
FRANKLIN CITY 201 – PRECINCT 2-1 075	1
FRANKLIN CITY 403 – SOUTHSIDE 076	1
FRANKLIN CITY 601 – PRECINCT 6-1 075	1
FRANKLIN COUNTY 204 – SANDY LEVEL 016	1
FRANKLIN COUNTY 401 – SOUTH LINDENWOOD 017	1
FRANKLIN COUNTY 601 – BOONES MILL 009	1
FREDERICK COUNTY 102 – OLD TOWN 029	1
FREDERICK COUNTY 103 – KERNSTOWN 029	1
FREDERICK COUNTY 201 – VIRGINIA AVENUE 029	1
FREDERICK COUNTY 202 – ALBIN 029	1
FREDERICK COUNTY 204 – NAIN 029	1
FREDERICK COUNTY 302 – NEFF’S TOWN 033	1
FREDERICK COUNTY 303 – WHITE HALL 029	1
FREDERICK COUNTY 402 – SHENANDOAH 010	1
FREDERICK COUNTY 403 – PARKIN’S MILL 010	1
FREDERICK COUNTY 502 – NEWTOWN 029	1
FREDERICK COUNTY 601 – MILLBROOK 033	1
FREDERICKSBURG CITY 201 – MONROE 099	1
FREDERICKSBURG CITY 201 – PRECINCT 1 – DISTRICT TWO 088	1
GILES COUNTY 102 – PRECINCT A-2 012	1
GILES COUNTY 202 – STAFFORDSVILLE 012	1
GLOUCESTER COUNTY 101 – FARMVILLE 060	1
GLOUCESTER COUNTY 102 – SALEM 098	1
GLOUCESTER COUNTY 502 – WALKER 098	1
GLOUCESTER COUNTY 510 – MEHFOUD 070	1
GOOCHLAND COUNTY 101 – SUBLETTS 065	1
GOOCHLAND COUNTY 201 – CARVER 057	1
GOOCHLAND COUNTY 302 – GOOCHLAND COURT HOUSE 2 065	1
GOOCHLAND COUNTY 303 – INNSBROOK 072	1
GOOCHLAND COUNTY 502 – BLAIR 056	1
GOOCHLAND COUNTY 702 – SOUTH ANNA 056	1
GRAYSON COUNTY 302 – FAIRVIEW 005	1
GRAYSON COUNTY 402 – PROVIDENCE 005	1
GREENE COUNTY 001 – NORTH SALEM NO 2 008	1
GREENE COUNTY 102 – MANAKIN 065	1
GREENE COUNTY 401 – MIDWAY 058	1
GREENSVILLE COUNTY 201 – PRECINCT 2-1 075	1
GREENSVILLE COUNTY 403 – PRECINCT 4-C 075	1
GREENSVILLE COUNTY 501 – PRECINCT 5-1 075	1
HALIFAX COUNTY 103 – REPUBLICAN GROVE 060	1
HALIFAX COUNTY 103 – SOUTH CLARKSVILLE 061	1
HALIFAX COUNTY 304 – VERNON HILL 060	1
HALIFAX COUNTY 701 – HYCO 060	1
HALIFAX COUNTY 703 – VIRGILINA 060	1
HAMPTON CITY 108 – KATHERINE JOHNSON 094	1
HAMPTON CITY 302 – YORKTOWN 096	1
HAMPTON CITY 308 – JEFFERSON 095	1
HANOVER COUNTY 001 – LEXINGTON 024	1
HANOVER COUNTY 203 – BELMONT 074	1
HANOVER COUNTY 218 – WILLARD 089	1
HANOVER COUNTY 301 – CAUSEWAY 056	1
HANOVER COUNTY 501 – MANGOHICK 097	1
HANOVER COUNTY 701 – SHELTONS MILL 056	1
HARRISONBURG CITY 101 – BROADWAY 026	1
HARRISONBURG CITY 201 – SINGERS GLEN 026	1
HARRISONBURG CITY 301 – KEEZLETOWN 026	1
HARRISONBURG CITY 301 – MILLWOOD 033	1
HARRISONBURG CITY 503 – MCGAHEYSVILLE 058	1
HENRICO COUNTY 077 – BROOKWOOD 084	1
HENRICO COUNTY 103 – GLEN ALLEN 072	1
HENRICO COUNTY 111 – LAKESIDE 072	1
HENRICO COUNTY 115 – STAPLES MILL 073	1
HENRICO COUNTY 201 – ADAMS 070	1
HENRICO COUNTY 203 – BELMONT 074	1
HENRICO COUNTY 206 – CENTRAL GARDENS 074	1
HENRICO COUNTY 207 – CHAMBERLAYNE 074	1
HENRICO COUNTY 208 – FAIRFIELD 074	1
HENRICO COUNTY 209 – GLEN LEA 074	1
HENRICO COUNTY 212 – HOLLYBROOK 074	1
HENRICO COUNTY 213 – HUNGARY 074	1
HENRICO COUNTY 222 – WILDER 074	1
HENRICO COUNTY 305 – NUCKOLS FARM 056	1
HENRICO COUNTY 307 – RIDGE 073	1
HENRICO COUNTY 311 – SHORT PUMP 056	1
HENRICO COUNTY 313 – STONEY RUN 072	1
HENRICO COUNTY 315 – TUCKER 073	1
HENRICO COUNTY 316 – COLONIAL TRAIL 056	1
HENRICO COUNTY 401 – QUIOCCASIN 073	1
HENRICO COUNTY 404 – FREEMAN 068	1
HENRICO COUNTY 404 – FREEMAN 073	1
HENRICO COUNTY 406 – GODWIN 072	1
HENRICO COUNTY 407 – LAKEWOOD 072	1
HENRICO COUNTY 413 – RIDGEFIELD 072	1
HENRICO COUNTY 415 – SKIPWITH 073	1
HENRICO COUNTY 416 – SPOTTSWOOD 073	1
HENRICO COUNTY 502 – BLAIR 056	1
HENRICO COUNTY 505 – DOREY 070	1
HENRICO COUNTY 509 – LABURNUM 074	1
HENRICO COUNTY 511 – MONTROSE 070	1
HENRICO COUNTY 512 – NINE MILE 074	1
HENRICO COUNTY 513 – PLEASANTS 074	1
HENRY COUNTY 005 – PRECINCT #5 016	1
HENRY COUNTY 201 – FIELDALE 016	1
HENRY COUNTY 203 – HORSEPASTURE #2 016	1
HENRY COUNTY 501 – BASSETT NUMBER ONE 009	1
HIGHLAND COUNTY 005 – BLUE GRASS 020	1
HOPEWELL CITY 101 – WARD ONE 062	1
HOPEWELL CITY 501 – WARD FIVE 062	1
ISLE OF WIGHT COUNTY 032 – HODGES MANOR ELEMENTARY SCHOOL 080	1
ISLE OF WIGHT COUNTY 201 – PRECINCT 2-1 075	1
ISLE OF WIGHT COUNTY 202 – CARROLLTON 064	1
ISLE OF WIGHT COUNTY 211 – CHRYSLER MUSEUM 089	1
ISLE OF WIGHT COUNTY 403 – LONGVIEW 064	1
ISLE OF WIGHT COUNTY 504 – ZUNI 064	1
ISLE OF WIGHT COUNTY 601 – COURTLAND 075	1
JAMES CITY COUNTY 101 – QUEENS LAKE 096	1
JAMES CITY COUNTY 103 – BERKELEY C 096	1
JAMES CITY COUNTY 104- BERKELEY D 093	1
JAMES CITY COUNTY 202 – JAMESTOWN B 096	1
JAMES CITY COUNTY 203 – JAMESTOWN C 096	1
JAMES CITY COUNTY 304 – POWHATAN D 096	1
JAMES CITY COUNTY 401 – STONEHOUSE A 096	1
JAMES CITY COUNTY 412 – PINCHBECK 073	1
JAMES CITY COUNTY 502 – NELLYSFORD 020	1
KING & QUEEN COUNTY 101 – OWENTON 098	1
KING & QUEEN COUNTY 503 – CHICKAHOMINY 074	1
KING GEORGE COUNTY 301 – PRECINCT 1 – DISTRICT THREE 088	1
KING GEORGE COUNTY 602 – SMITH STATION 054	1
KING WILLIAM COUNTY 101 – WEST POINT 098	1
KING WILLIAM COUNTY 301 – AYLETT 097	1
KING WILLIAM COUNTY 401 – MANQUIN 097	1
LANCASTER COUNTY 301 – PRECINCT 3-1 099	1
LANCASTER COUNTY 302 – PRECINCT 3-2 099	1
LANCASTER COUNTY 501 – PRECINCT 5-1 099	1
LEXINGTON CITY 101 – AIRPORT 024	1
LOUDOUN COUNTY 016 – LYON VILLAGE 048	1
LOUDOUN COUNTY 209 – POTOMAC FALLS 034	1
LOUDOUN COUNTY 303 – HILLSBORO 033	1
LOUDOUN COUNTY 305 – PHILOMONT 010	1
LOUDOUN COUNTY 312 – BRIAR WOODS 010	1
LOUDOUN COUNTY 314 – LEGACY 087	1
LOUDOUN COUNTY 401 – WEST LOVETTSVILLE 033	1
LOUDOUN COUNTY 401 – WHITE POST 010	1
LOUDOUN COUNTY 403 – LUCKETTS 033	1
LOUDOUN COUNTY 407 – HARPER PARK 010	1
LOUDOUN COUNTY 508 – BALLS BLUFF 033	1
LOUDOUN COUNTY 622 – FARMWELL STATION 032	1
LOUDOUN COUNTY 707 – CLAUDE MOORE PARK 087	1
LOUDOUN COUNTY 709 – MIRROR RIDGE 087	1
LOUDOUN COUNTY 710 – STERLING 087	1
LOUDOUN COUNTY 818 – BROAD RUN 032	1
LOUDOUN COUNTY 820 – BELMONT STATION 032	1
LOUISA COUNTY 101 – PALMYRA 058	1
LOUISA COUNTY 102 – MECHANICSVILLE 056	1
LOUISA COUNTY 201 – COLUMBIA 065	1
LOUISA COUNTY 202 – LOUISA #2 056	1
LOUISA COUNTY 701 – SHELTONS MILL 056	1
LUNENBURG COUNTY 301 – ROSEBUD 075	1
LUNENBURG COUNTY 402 – PLEASANT GROVE 061	1
LUNENBURG COUNTY 501 – REEDY CREEK 061	1
LUNENBURG COUNTY 501 – SOUTH HILL 061	1
LUNENBURG COUNTY 502 – PEOPLES COMMUNITY CENTER 061	1
LUNENBURG COUNTY 601 – HOUNDS CREEK 075	1
LYNCHBURG CITY 101 – BROOKVILLE 022	1
LYNCHBURG CITY 102 – FIRST WARD SECOND PRECINCT 023	1
LYNCHBURG CITY 102 – NEW LONDON 022	1
LYNCHBURG CITY 201 – MONROE 099	1
LYNCHBURG CITY 201 – WALKER 022	1
LYNCHBURG CITY 301 – THIRD WARD FIRST PRECINCT 022	1
LYNCHBURG CITY 303 – THIRD WARD THIRD PRECINCT 022	1
LYNCHBURG CITY 401 – CUNNINGHAM 058	1
LYNCHBURG CITY 501 – SPRING HILL 022	1
LYNCHBURG CITY 506 – MOUNT VERNON 017	1
MADISON COUNTY 006 – WOLFTOWN 030	1
MANASSAS CITY 002 – WEEMS 050	1
MANASSAS CITY 004 – HAYDON 050	1
MANASSAS CITY 301 – GRIFFIS 028	1
MANASSAS CITY 413 – RIDGEFIELD 072	1
MECKLENBURG COUNTY 103 – SOUTH CLARKSVILLE 061	1
MECKLENBURG COUNTY 301 – BRACEY 061	1
MECKLENBURG COUNTY 502 – PEOPLES COMMUNITY CENTER 075	1
MECKLENBURG COUNTY 701 – CHASE CITY 061	1
MECKLENBURG COUNTY 702 – MIDWAY 060	1
MECKLENBURG COUNTY 802 – BLUESTONE 061	1
MIDDLESEX COUNTY 101 – WEST POINT 098	1
MIDDLESEX COUNTY 203 – JAMESTOWN C 096	1
MIDDLESEX COUNTY 501 – WILTON 098	1
MONTGOMERY COUNTY 001 – EAST PRECINCT 012	1
MONTGOMERY COUNTY 058 – GLENWOOD 021	1
MONTGOMERY COUNTY 101 – PRECINCT A-1 012	1
MONTGOMERY COUNTY 201 – PRECINCT B-1 012	1
MONTGOMERY COUNTY 401 – PRECINCT D-1 007	1
MONTGOMERY COUNTY 402 – PRECINCT D-2 007	1
MONTGOMERY COUNTY 503 – PRECINCT E-3 007	1
NELSON COUNTY 201 – LOVINGSTON 059	1
NELSON COUNTY 216 – MOODY 074	1
NELSON COUNTY 401 – ROSELAND 020	1
NELSON COUNTY 502 – NELLYSFORD 020	1
NEWPORT NEWS CITY 017 – OCEAN PARK 083	1
NEWPORT NEWS CITY 107 – RICHNECK 093	1
NEWPORT NEWS CITY 201 – BLAND 094	1
NEWPORT NEWS CITY 209 – HILTON 095	1
NEWPORT NEWS CITY 210 – KNOLLWOOD MEADOWS 094	1
NEWPORT NEWS CITY 215 – WARWICK 094	1
NEWPORT NEWS CITY 218 – KILN CREEK 093	1
NEWPORT NEWS CITY 301 – SEAFORD 096	1
NEWPORT NEWS CITY 302 – PRECINCT 3-2 099	1
NEWPORT NEWS CITY 303 – CARVER 095	1
NEWPORT NEWS CITY 305 – DOWNTOWN 095	1
NEWPORT NEWS CITY 312 – NEWSOME PARK 095	1
NORFOLK CITY 045 – TIMBERLAKE 021	1
NORFOLK CITY 101 – GRANBY 079	1
NORFOLK CITY 101 – GRANBY 100	1
NORFOLK CITY 203 – GHENT SQUARE 089	1
NORFOLK CITY 207 – LAMBERT’S POINT 089	1
NORFOLK CITY 209 – HILTON 095	1
NORFOLK CITY 212 – PARK PLACE 089	1
NORFOLK CITY 215 – SUBURBAN PARK 100	1
NORFOLK CITY 218 – WILLARD 079	1
NORFOLK CITY 309 – NORVIEW 090	1
NORFOLK CITY 402 – BERKLEY 089	1
NORFOLK CITY 404 – CAMPOSTELLA 089	1
NORFOLK CITY 408 – EASTON 090	1
NORFOLK CITY 411 – RUFFNER ACADEMY 089	1
NORFOLK CITY 501 – BAYVIEW 090	1
NORFOLK CITY 506 – OCEAN VIEW CENTER 100	1
NORTHUMBERLAND COUNTY 501 – PRECINCT 5-1 099	1
NORTON CITY 004 – FOURTH WARD 005	1
NOTTOWAY COUNTY 201 – PRECINCT 2-1 061	1
NOTTOWAY COUNTY 401 – PRECINCT 4-1 061	1
ORANGE COUNTY 001 – OAK PARK 030	1
ORANGE COUNTY 101 – PRECINCT 1 – DISTRICT ONE 088	1
ORANGE COUNTY 201 – 2A 099	1
ORANGE COUNTY 201 – TWO WEST 030	1
ORANGE COUNTY 302 – THREE EAST 030	1
PATRICK COUNTY 102 – FLATRIDGE 005	1
PATRICK COUNTY 302 – LIBERTY 009	1
PETERSBURG CITY 101 – FIRST WARD FIRST PRECINCT 063	1
PETERSBURG CITY 601 – SIXTH WARD FIRST PRECINCT 063	1
PITTSYLVANIA COUNTY 103 – TWIN SPRINGS 016	1
PITTSYLVANIA COUNTY 105 – CHATHAM 016	1
PITTSYLVANIA COUNTY 108 – WEST BLAIRS 016	1
PITTSYLVANIA COUNTY 207 – GRETNA 016	1
PITTSYLVANIA COUNTY 305 – RICEVILLE 016	1
POQUOSON CITY 001 – CENTRAL 091	1
POQUOSON CITY 101 – BERLIN 075	1
POQUOSON CITY 202 – KILN CREEK 093	1
PORTSMOUTH CITY 014 – BRIGHTON ELEMENTARY SCHOOL 080	1
PORTSMOUTH CITY 022 – ST. MARK DELIVERANCE CENTER 080	1
PORTSMOUTH CITY 028 – LAKEVIEW ELEMENTARY SCHOOL 080	1
PORTSMOUTH CITY 037 – CHURCHLAND MIDDLE SCHOOL 080	1
PORTSMOUTH CITY 039 – CHURCHLAND PRIMARY AND INTERMEDIATE SCHOOL 079	1
POWHATAN COUNTY 401 – POWHATAN COURTHOUSE 065	1
POWHATAN COUNTY 413 – RIDGEFIELD 072	1
POWHATAN COUNTY 503 – TOBACCOVILLE 065	1
PRINCE EDWARD COUNTY 201 – LOCKETT 060	1
PRINCE EDWARD COUNTY 301 – LEIGH 060	1
PRINCE EDWARD COUNTY 501 – PRECINCT 5 061	1
PRINCE GEORGE COUNTY 101 – RICHARD BLAND 064	1
PRINCE GEORGE COUNTY 103 – UNION BRANCH 064	1
PRINCE GEORGE COUNTY 202 – SUTHERLAND 063	1
PRINCE GEORGE COUNTY 205 – JEFFERSON PARK 062	1
PRINCE GEORGE COUNTY 205 – JEFFERSON PARK 064	1
PRINCE WILLIAM COUNTY 004 – HAYDON 050	1
PRINCE WILLIAM COUNTY 006 – WOLFTOWN 030	1
PRINCE WILLIAM COUNTY 024 – LARKSPUR 085	1
PRINCE WILLIAM COUNTY 101 – COURTHOUSE 099	1
PRINCE WILLIAM COUNTY 102 – PRECINCT 1-2 099	1
PRINCE WILLIAM COUNTY 103 – GLENKIRK 013	1
PRINCE WILLIAM COUNTY 103 – SIMPSON 088	1
PRINCE WILLIAM COUNTY 122 – HUTCHISON FARM 087	1
PRINCE WILLIAM COUNTY 201 – MONROE 099	1
PRINCE WILLIAM COUNTY 202 – AIRLIE 018	1
PRINCE WILLIAM COUNTY 202 – ALBIN 029	1
PRINCE WILLIAM COUNTY 210 – PENN 051	1
PRINCE WILLIAM COUNTY 301 – DAHLGREN 099	1
PRINCE WILLIAM COUNTY 301 – PRECINCT 1 – DISTRICT THREE 088	1
PRINCE WILLIAM COUNTY 303 – BEALETON 018	1
PRINCE WILLIAM COUNTY 305 – PATTIE 031	1
PRINCE WILLIAM COUNTY 311 – SWANS CREEK 002	1
PRINCE WILLIAM COUNTY 320 – STONE HILL 087	1
PRINCE WILLIAM COUNTY 402 – FOUR EAST 030	1
PRINCE WILLIAM COUNTY 409 – CLARKES GAP 033	1
PRINCE WILLIAM COUNTY 622 – FARMWELL STATION 032	1
PULASKI COUNTY 201 – DRAPER 007	1
PULASKI COUNTY 203 – NEWBERN 007	1
RADFORD CITY 004 – NEW RIVER PRECINCT 012	1
RADFORD CITY 102 – NEW RIVER 012	1
RADFORD CITY 103 – PRECINCT A-3 012	1
RAPPAHANNOCK COUNTY 101 – WASHINGTON 018	1
RAPPAHANNOCK COUNTY 201 – AMISSVILLE 018	1
RAPPAHANNOCK COUNTY 401 – SCRABBLE 018	1
RAPPAHANNOCK COUNTY 502 – FLINT HILL 018	1
RICHMOND CITY 101 – FARMVILLE 060	1
RICHMOND CITY 101 – OWENTON 098	1
RICHMOND CITY 106 – HERMITAGE 072	1
RICHMOND CITY 110 – JOHNSON 073	1
RICHMOND CITY 111 – LAKESIDE 072	1
RICHMOND CITY 209 – GLEN LEA 074	1
RICHMOND CITY 220 – RATCLIFFE 074	1
RICHMOND CITY 304 – JACKSON DAVIS 073	1
RICHMOND CITY 309 – SADLER 056	1
RICHMOND CITY 506 – EANES 070	1
RICHMOND CITY 510 – MEHFOUD 070	1
RICHMOND CITY 514 – ROLFE 070	1
RICHMOND CITY 515 – DAVIS 066	1
RICHMOND CITY 702 – PRECINCT G-2 012	1
ROANOKE CITY 014 – Crystal Spring 011	1
ROANOKE CITY 015 – Grandin Court 017	1
ROANOKE CITY 019 – Forest Park 011	1
ROANOKE CITY 202 – BURLINGTON 017	1
ROANOKE CITY 406 – MOUNT PLEASANT 017	1
ROANOKE CITY 506 – MOUNT VERNON 017	1
ROANOKE COUNTY 102 – GREENFIELD 019	1
ROANOKE COUNTY 105 – PETERS CREEK 017	1
ROANOKE COUNTY 106 – GREEN HILL 008	1
ROANOKE COUNTY 204 – BOTETOURT SPRINGS 017	1
ROANOKE COUNTY 206 – HOLLINS 017	1
ROANOKE COUNTY 305 – CASTLE ROCK 008	1
ROANOKE COUNTY 402 – BONSACK 017	1
ROANOKE COUNTY 405 – NORTH LINDENWOOD 017	1
ROCKBRIDGE COUNTY 102 – BEN SALEM 024	1
ROCKBRIDGE COUNTY 103 – PLANK ROAD 024	1
ROCKBRIDGE COUNTY 301 – MAURY RIVER 024	1
ROCKBRIDGE COUNTY 303 – WINDSOR HILLS 017	1
ROCKBRIDGE COUNTY 504 – ROCKBRIDGE 024	1
ROCKINGHAM COUNTY 101 – FARMVILLE 060	1
ROCKINGHAM COUNTY 102 – TIMBERVILLE 026	1
ROCKINGHAM COUNTY 105 – LACEY SPRING 015	1
ROCKINGHAM COUNTY 108 – LITTLE NORTH MOUNTAIN 026	1
ROCKINGHAM COUNTY 201 – SINGERS GLEN 026	1
ROCKINGHAM COUNTY 301 – KEEZLETOWN 026	1
ROCKINGHAM COUNTY 302 – PORT REPUBLIC 025	1
ROCKINGHAM COUNTY 401 – WEST BRIDGEWATER 025	1
ROCKINGHAM COUNTY 402 – MONTEZUMA 025	1
ROCKINGHAM COUNTY 404 – NORTH RIVER 025	1
ROCKINGHAM COUNTY 406 – EAST BRIDGEWATER 025	1
ROCKINGHAM COUNTY 501 – ELKTON 058	1
ROCKINGHAM COUNTY 504 – SOUTH FORK 058	1
ROCKINGHAM COUNTY 505 – STONY RUN 026	1
RUSSELL COUNTY 101 – MOCCASIN 004	1
RUSSELL COUNTY 302 – DAUGHERTY 004	1
RUSSELL COUNTY 303 – NEW GARDEN 003	1
RUSSELL COUNTY 403 – ST PAUL 004	1
RUSSELL COUNTY 601 – EAST LEBANON 004	1
SALEM CITY 004 – WEST SALEM 008	1
SALEM CITY 010 – HIDDEN VALLEY 008	1
SHENANDOAH COUNTY 101 – ORKNEY SPRINGS 015	1
SMYTH COUNTY 502 – WASSONA 006	1
SOUTHAMPTON COUNTY 102 – WALLER MILL 096	1
SOUTHAMPTON COUNTY 501 – HUNTERDALE 075	1
SPOTSYLVANIA COUNTY 101 – COURTHOUSE 099	1
SPOTSYLVANIA COUNTY 201 – PRECINCT 1 – DISTRICT TWO 088	1
SPOTSYLVANIA COUNTY 202 – SOUTH MADISON 055	1
SPOTSYLVANIA COUNTY 301 – PRECINCT 1 – DISTRICT THREE 088	1
SPOTSYLVANIA COUNTY 303 – RIVERBEND 088	1
SPOTSYLVANIA COUNTY 401 – DAWN 055	1
SPOTSYLVANIA COUNTY 402 – FOUR EAST 030	1
SPOTSYLVANIA COUNTY 502 – MILFORD 055	1
STAFFORD COUNTY 019 – ROSSLYN 048	1
STAFFORD COUNTY 102 – ROCKY RUN 088	1
STAFFORD COUNTY 103 – SIMPSON 088	1
STAFFORD COUNTY 202 – ROSEVILLE 002	1
STAFFORD COUNTY 301 – PRECINCT 1 – DISTRICT THREE 088	1
STAFFORD COUNTY 302 – REMINGTON 088	1
STAFFORD COUNTY 403 – BROOKE 028	1
STAFFORD COUNTY 501 – GRAFTON 028	1
STAFFORD COUNTY 501 – PRECINCT 5-1 099	1
STAFFORD COUNTY 603 – WHITE OAK 028	1
STAFFORD COUNTY 604 – ENGLAND RUN 028	1
STAFFORD COUNTY 702 – WHITSON 002	1
STAFFORD COUNTY 703 – HAMPTON 088	1
STAUNTON CITY 204 – MT CLINTON 026	1
STAUNTON CITY 301 – FORT DEFIANCE 025	1
STAUNTON CITY 301 – WARD NO 3 020	1
SUFFOLK CITY 020 – NOBLE STREET BAPTIST CHURCH 080	1
SUFFOLK CITY 101 – Key Recreation 057	1
SUFFOLK CITY 102 – CYPRESS CREEK 064	1
SUFFOLK CITY 102 – DRIVER 076	1
SUFFOLK CITY 202 – CHUCKATUCK 076	1
SUFFOLK CITY 204 – HILLPOINT 076	1
SUFFOLK CITY 302 – JOHN F KENNEDY 076	1
SUFFOLK CITY 304 – NANSEMOND RIVER 076	1
SUFFOLK CITY 305 – SHOULDERS HILL 076	1
SUFFOLK CITY 402 – WHALEYVILLE 064	1
SUFFOLK CITY 404 – BOOKER T WASHINGTON 076	1
SUFFOLK CITY 603 – ELEPHANTS FORK/WESTHAVEN 076	1
SUFFOLK CITY 604 – WILROY 076	1
SUFFOLK CITY 605 – HOLLYWOOD 076	1
SUFFOLK CITY 702 – HARBOURVIEW 076	1
SUSSEX COUNTY 101 – WAVERLY 075	1
SUSSEX COUNTY 401 – PRECINCT 4-1 075	1
SUSSEX COUNTY 403 – CHERRY HILL 063	1
TAZEWELL COUNTY 109 – BISHOP 003	1
TAZEWELL COUNTY 204 – CLEAR FORK 003	1
VIRGINIA BEACH CITY 004 – LINKHORN 082	1
VIRGINIA BEACH CITY 006 – ALANTON 082	1
VIRGINIA BEACH CITY 012 – PLAZA 082	1
VIRGINIA BEACH CITY 026 – FAIRFIELD 085	1
VIRGINIA BEACH CITY 030 – RED WING 081	1
VIRGINIA BEACH CITY 038 – WITCHDUCK 083	1
VIRGINIA BEACH CITY 048 – WOLFSNARE 082	1
VIRGINIA BEACH CITY 049 – LYNNHAVEN 082	1
VIRGINIA BEACH CITY 063 – CULVER 081	1
VIRGINIA BEACH CITY 070 – CORPORATE LANDING 081	1
VIRGINIA BEACH CITY 076 – VILLAGE 085	1
VIRGINIA BEACH CITY 080 – CHIMNEY HILL 084	1
VIRGINIA BEACH CITY 086 – HAYGOOD 083	1
VIRGINIA BEACH CITY 102 – DRIVER 076	1
VIRGINIA BEACH CITY 401 – 4A 099	1
VIRGINIA BEACH CITY 403 – STONEHOUSE C 096	1
VIRGINIA BEACH CITY 413 – POPLAR HALLS 090	1
WARREN COUNTY 102 – OLD TOWN 029	1
WARREN COUNTY 102 – OTTERBURN 015	1
WARREN COUNTY 402 – TOWN – WEST SHENANDOAH 029	1
WARREN COUNTY 502 – FLINT HILL 018	1
WASHINGTON COUNTY 102 – WEST ABINGDON 004	1
WASHINGTON COUNTY 203 – HAYTERS GAP 005	1
WASHINGTON COUNTY 204 – WOODLAND HILLS 004	1
WASHINGTON COUNTY 501 – RHEA VALLEY 005	1
WASHINGTON COUNTY 601 – BURSON PLACE 004	1
WASHINGTON COUNTY 702 – WALLACE 004	1
WAYNESBORO CITY 202 – WALKER 057	1
WESTMORELAND COUNTY 101 – COURTHOUSE 099	1
WESTMORELAND COUNTY 201 – PRECINCT 2-1 099	1
WESTMORELAND COUNTY 301 – PRECINCT 3-1 099	1
WILLIAMSBURG CITY 102 – WALLER MILL 096	1
WINCHESTER CITY 301 – WAR MEMORIAL 029	1
WINCHESTER CITY 302 – NEFF’S TOWN 033	1
WINCHESTER CITY 402 – SHENANDOAH 010	1
WISE COUNTY 101 – APPALACHIA 001	1
WISE COUNTY 104 – WEST POUND 004	1
WISE COUNTY 301 – BIG STONE GAP 001	1
WYTHE COUNTY 203 – NEWBERN 007	1
WYTHE COUNTY 501 – JACKSON MEMORIAL 006	1
YORK COUNTY 102 – WALLER MILL 096	1

Election Data Analysis Election Forensics Election Integrity Interesting programming technical

The 300K VA Ballots Outstanding and At-Risk Claim is Incorrect.

Post author By Jonathan Lareau
Post date November 1, 2021

There’s a (IMO frivolous) lawsuit by Mark Elias (here) against the USPO that is causing people to think that there are > 300K outstanding mail-in ballots in VA. According to the VA Dept of Elections data, this is just factually incorrect. There are not 300K outstanding absentee ballots floating around. There is < 100K as per the 11/01/2021 DAL file entries. (Light blue line, logarithmic y axis)

Of the 3 Localities listed in the lawsuit, from the 11/01/2021 DAL File:

	ALBEMERLE COUNTY	JAMES CITY COUNTY	PORTSMOUTH CITY
Total Registered Voters	81738	61961	66696
Total Outstanding Mail In Ballots	2545	1061	1151
Registered / Outstanding * 100	3.1%	1.7%	1.7%

The graph of the breakouts of these 3 counties over time as the DAL files have been updated during the early voting period is shown below. As we see increases in the number of mail in ballots that are in a status state of “Marked” or “Pre-Processed”, we see corresponding decreases in the outstanding “Issued” ballots in all 3 localities. We are NOT seeing a huge buildup of “Issued” ballots that are backlogged as claimed in the lawsuit corresponding to an “October Slowdown” by the USPO. His lawsuit is bunk.

Election Data Analysis Election Forensics Election Integrity Interesting programming technical

GALAX CITY “Marked +/or Pre-Processed” Vote Tally Decreases … why?

Post author By Jonathan Lareau
Post date November 1, 2021

I have been working with a number of different groups for GOTV efforts for the 2021 VA Election, as as such I have been archiving and trending the Daily Absentee List (DAL) data files for a while now. One curious case that I’d love to get somebody at VA ELECT to explain, is why the set of (“Marked” +/or “Pre-Processed”) Ballots for GALAX City has suddenly been reduced to near zero.

As background, the DAL is effectively a transaction log of the status of all early and absentee ballots in VA. When a qualified voter requests a by-mail absentee ballot and it is sent to them a DAL record is created in an “Issued” state. Once it is received the record is updated to “Marked”, and once the ballot has been opened and scanned into a tabulator it is updated to “Pre-Processed”.

In the chart below we can see the number of issued ballots increasing, then decreasing as ballots are received and updated to “Marked” or “Pre-Processed”, but then suddenly (starting with the Oct 26th DAL files) we see the “MarkedOrPre” trace drop to near zero. The only line in this graph that I would ever expect to see decreasing is the number of outstanding “Issued” ballots. So … whats going on here?

Election Data Analysis Election Forensics Election Integrity Interesting programming technical

VA 2020 Election Analysis Report (v5)

Post author By Jonathan Lareau
Post date October 21, 2021

Adding on to my previous report (old version is here).

Fixed a few typos and formatting issues.
Added some discussion about the fact that the VA DOE did correct the turnout statistic error I found, but did not make any sort of statement or explanation as to why the error was there in the first place; why did it go undiscovered for nearly a year until I pointed it out; what procedures and policies are in place to make sure errors like this don’t happen again?
Added a section documenting the discovery that a small number of public records have been retroactively adjusted and specific entries are now missing from the public archives regarding the registered voter totals.

VA-2020-Election-Analysis-v5 Download

Election Data Analysis Election Forensics Election Integrity Interesting programming technical

Comparison of 2020 and 2021 Absentee Breakouts in VA

Post author By Jonathan Lareau
Post date October 21, 2021

I got asked a question earlier this evening as to how the current 2021 VA election early vote/absentee data was shaping up in comparison to the 2020, so I did some quick processing and plotting of the Daily Absentee List (DAL) from just after the 2020 election (11-09-2020), and the current DAL as of today (10-21-2021).

The below graphs plot the APP_STATUS=”Approved” entries in the DAL, broken out by BALLOT_STATUS and plotted vs their BALLOT_RECEIPT_DATE. One major difference is that we haven’t had any Federal Write-In Absentee Ballots (FWAB) entered into the DAL in 2021 yet that have a valid BALLOT_RECEIPT_DATE, and the 2020 FWAB counts had a very different general curve than the other ballots. We also had a little less than 1000 ballots entered “On Machine” before early voting started in 2020. We see ballots issued earlier in the year for 2021, but no major “On Machine” counts. Note these graphs are logarithmic in the y-axis for easier viewing, and I had to discard 660 entries for 2020 and 11 entries for 2021 because the BALLOT_RECEIPT_DATE was invalid.

Election Data Analysis Election Forensics Election Integrity Interesting programming technical

More Details on “Ideal” Fingerprint Computations

Post author By Jonathan Lareau
Post date September 24, 2021

Per request by a reviewer of my most recent election irregularities report in VA (here), here’s a little more technical detail as to how the “ideal” model is computed in accordance with the original 2012 National Academy of Sciences paper that I based this work off of.

The generalized summary in my report for VA reads as follows:

“The upper right image was computed per the NAS paper; the bottom left image shows what an idealized model of the data could or should look like, based on the reported voter turnout and vote share for the winner. This ideal model is allowed to have up to 3 Gaussian lobes based on the peak locations and standard deviations in the reported Virginia results.”

While that description is absolutely accurate, it glosses over some of the implementation as I didn’t want the reader to go all glassy-eyed on me! A more explicit technical definition is as follows: All of the localized maximal peaks in the 2D histogram that are above pThresh (~= 0.7) x the value of the global maximum peak are used as the centroids of a Gaussian Mixture model, with shared covariance matrix equal to 1.5 x sqrt of the covariance matrix of all of the data points. (Thats a lot of mathematics packed into one sentence, but its accurate!) In the case of the VA per county per cong district data this give us either 2 or 3 peaks dependent on the value that is used for the pThresh threshold. The value of 0.7 was chosen after observing results from multiple states data that I have been doing fingerprint analysis on. The MATLAB imregionalmax(…) function from the Image Processing Toolbox is used to find the candidate localized peaks, and the gmdistribution(…) function from the Statistics toolbox generated the final idealized model.

% HBf is the 2D Histogram image
BW = imregionalmax(HBf);
v = HBf(BW);
[r,c] = find(BW.*HBf >=  max(v(:))*pThresh);
mu = [r,c];
s = 1.5;

cv = diag(diag(s*sqrt(cov(rawData))));
GMModel = gmdistribution(mu,cv);

The end result of this is shown below (bottom left) with the Bayesian Information Criterion (BIC) and number of Gaussian components listed in the title of the bottom left “ideal” plot.

Election Data Analysis Election Forensics Election Integrity Interesting technical

VA 2020 Election Analysis Report

Post author By Jonathan Lareau
Post date September 9, 2021

Finally. This has been a long time in the making, but here is my summarized report on the most significant VA 2020 General Election irregularities that I’ve discovered. All of this information is presented in detail in previous posts on this site, as well as cataloging many other issues, but I’ve collected the major points here to try and make things easily digestible and accessible to those who are interested.

Special thanks to everyone that helped in putting this together, acquiring deciphering and collating data, performing peer review, etc. I have tried to be as meticulous and as transparent as possible so that others can recreate my results at every stage if they wish to validate.

Note there is a newer updated version of this report (here).

VA-2020-Election-Analysis-v4 Download

Election Data Analysis Election Forensics Election Integrity Interesting programming technical

NH 2020 Election Fingerprint

Post author By Jonathan Lareau
Post date September 4, 2021

Background:

The US National Academy of Sciences (NAS) published a paper in 2012 titled “Statistical detection of systematic election irregularities.” [1] The paper asked the question, “How can it be distinguished whether an election outcome represents the will of the people or the will of the counters?” The study reviewed the results from elections in Russia and other countries, where widespread fraud was suspected. The study was published in the proceedings of the National Academy of Sciences as well as referenced in multiple election guides by USAID [2][3], among other citations.

The study authors’ thesis was that with a large sample of the voting data, they would be able to see whether or not voting patterns deviated from the voting patterns of elections where there was no fraud. The results of their study proved that there were indeed significant deviations from the expected, normal voting patterns in the elections where fraud was suspected.

Statistical results are often graphed, to provide a visual representation of how normal data should look. A particularly useful visual representation of election data is the election fingerprint. When used to analyze election data, the election fingerprint typically analyzes the votes for the winner versus voter turnout by voting district. The expected shape of the fingerprint is of that of a 2D Gaussian (a.k.a. “Normal”) distribution [4]. (See this MIT News article for a great additional description and primer on the Gaussian or Normal distribution: https://news.mit.edu/2012/explained-sigma-0209)

Here is an example reprinted from the referenced National Academy of Sciences paper:

The actual election results in Russia, Uganda and Switzerland appear in the left column, the right column is the expected appearance in a fair election with little fraud, and the middle column is the researchers’ model with fraud included.

As you can see, the election in Switzerland shows a range of voter turnout, from approximately 30 – 70% across voting districts, and a similar range of votes for the winner.

What do the clusters mean in the Russia 2011 and 2012 elections? Of particular concern are the top right corners, showing nearly 100% turnout of voters, and nearly 100% of them voted for the winner.

Both of those events (more than 90% of registered voters turning out to vote and more than 90% of the voters voting for the winner) are statistically improbable, even for very contested elections. Election results that show a strong linear streak away from the main fingerprint lobe indicates ‘ballot stuffing,’ where ballots are added at a specific rate. Voter turnout over 100% indicates ‘extreme fraud’. [1][5]

Election results with ‘outliers’ – results that fall outside of normal voting patterns – are not in and of themselves definitive proof of outright fraud. But additional reviews of voting patterns and election results should be conducted whenever deviations from normal patterns occur in an election. Additionally it should be noted that “the absence of evidence is not the evidence of absence”: Election Fingerprints that look otherwise normal might still have underlying issues that are just simply not readily apparent with this view of the data.

Using this studies methodology, in late 2020 and 2021, multiple researchers in the US have applied the same analysis to the US 2020 election results, as well as the results of previous elections.

The US 2020 Election – New Hampshire:

Source Data:

Registered Voter Data: https://sos.nh.gov/media/00lg4swb/names-on-checklist-general-2020.xlsx
Total Regular and Absentee Ballots Cast: https://sos.nh.gov/media/yi4fonny/ballots-cast-2020-general.xls
Vote Totals: https://sos.nh.gov/media/yjmp5qmd/president-2020.xls
Write-In Totals: https://sos.nh.gov/media/wv3m4jne/presidential-write-ins-2020.pdf
Records of Voter Rolls Pre-Election Day, On Election Day, and marked as Absentee. (Note that due to personal privacy considerations, this raw dataset is not openly published and the raw data must be obtained via request. The summaries of this dataset is included in the “2020-NH-Combined-Data.csv” file included below)

Election Fingerprint:

The upper right image in the following graphic is the computed election fingerprint, computed according to the NAS paper and using official state reported voter turnout and votes for the statewide winner. The color scale moves from precincts with low counts as deep blue, to precincts with high numbers represented as bright yellow. Note that a small blurring filter was applied to the computed image for ease of viewing small isolated histogram hits.

The bottom left image of the graphic shows what an “idealized” model of the data could look like. The upper right image was computed per the NAS paper; the bottom left image shows what an idealized mixture-of-Gaussian model of the data should look like, based on the reported voter turnout and vote share for the winner.

The top-left and bottom-right plots show the sum of the rows and columns of the fingerprint image. The top-left graph corresponds to the sum of the rows in the upper right image and is the histogram of the vote share for Biden across precincts. The bottom right plot corresponds sum of the columns of the upper right image, and is the histogram of the % turnout across the precincts.

Observations/Conclusions:

There does not appear to be any majorly distinct linear correlations, over 100% turnout precincts, or otherwise major red flags even though there is some patterned noise. The distribution is very large and diffuse, and has a definite skew, which is curious, but not necessarily indicative.
There are a small number of outlier precincts outside of the main distribution lobe, most notably the cluster along the 40% turnout line (Lempster, Newport & Claremont Ward 3), and two precincts above 90% turnout (Randolph & Ellsworth).
There are at least two major peaks in the main lobe, which is consistent with the theory of a split electorate.
The % Vote Share for Biden plot (Upper-Left) is “lop-sided” and shows a distinct skew in the data above the 40% Vote Share mark.
Looking at the difference between the Total Reported Votes from Source B and Total Votes count from official Source C shows 10,666 unaccounted for votes. The total number of Write-In votes from Source D was only 1158 and not nearly enough to account for this difference.
Looking at the difference between the registered voters from Source E and the Registered voters from Source A, there is a difference of 122,248 registrations.

References:

[1] “Statistical detection of election irregularities” Peter Klimek, Yuri Yegorov, Rudolf Hanel, Stefan Thurner Proceedings of the National Academy of Sciences Oct 2012, 109 (41) 16469-16473; DOI: 10.1073/pnas.1210722109 (https://www.pnas.org/content/109/41/16469)

[2] USAID: Assessing and Verifying Election Results: A Decision Makers Guide to Parallel Vote Tabulation and Other Tools (http://web.archive.org/web/20201118021847/https://pdf.usaid.gov/pdf_docs/PA00KGWR.pdf)

[3] USAID: A guide to Election Forensics (http://web.archive.org/web/20210501091306/https://pdf.usaid.gov/pdf_docs/PA00MXR7.pdf)

[4] Multivariate Normal Distribution – Wikipedia (https://en.wikipedia.org/wiki/Multivariate_normal_distribution)

[5] Mebane, Walter R. and Kalinin, Kirill, Comparative Election Fraud Detection (2009). APSA 2009 Toronto Meeting Paper, Available at SSRN: https://ssrn.com/abstract=1450078

Data Files:

2020-NH-Combined-Data Download

NH-Election-Fingerprint_TabulatedResults Download

NH-Election-Fingerprint-analysis Download

Recent Posts

Recent Comments

Archives

Categories