Statistical Detection of Irregularities via Cast Vote Records

There has been a good amount of commotion regarding cast vote records (CVRs) and their importance lately. I wanted to take a minute and try and help explain why these records are so important, and how they provide a tool for statistical inspection of election data. I also want to try and dispel any misconceptions as to what they can or can’t tell us.

I have been working with other local Virginians to try and get access to complete CVRs for about 6 months (at least) in order to do this type of analysis. However, we had not had much luck in obtaining real data (although we did get a partial set from PWC primaries but it lacked the time-sequencing information) to evaluate until after Jeff O’Donnell (a.k.a. the Lone Raccoon) and Walter Dougherity did a fantastic presentation at the Mike Lindell Moment of Truth Summit on CVRs and their statistical use. That presentation seems to have broken the data logjam, and was the impetus for writing this post.

Just like the Election Fingerprint analysis I was doing earlier that highlighted statistical anomalies in election data, this CVR analysis is a statistics based technique that can help inform us as to whether or not the election data appears consistent with expectations. It only uses the official results as provided by state or local election authorities and relies on standard statistical principles and properties. Nothing more. Nothing less.

What is a cast vote record?

A cast vote record is part of the official election records that need to be maintained in order for election systems to be auditable. (see: 52 USC 21081 , NIST CVR Standard, as well as the Virginia Voting Systems Certification Standards) They can have many different formats depending on equipment vendor, but they are effectively a record of each ballot as it was recorded by the equipment. Each row in a CVR data table should represent a single ballot being cast by a voter and contain, at minimum, the time (or sequence number) when the ballot was cast, the ballot type, and the result of each race. Other data might also be included such as which precinct and machine performed the scanning/recording of the ballot, etc. Note that “cast vote records” are sometimes also called “cast voter records”, “ballot reports” or a number of other different names depending on the publication or locality. I will continue to use the “cast vote record” language in this document for consistency.

Why should we care?

The reason these records are so important, is based on statistics and … unfortunately … involves some math to fully describe. But to make this easier, let’s try first to walk through a simple thought experiment. Let’s pretend that we have a weighted, or “trick” coin, that when flipped it will land heads 53% of the time and land tails 47% of the time. We’re going to continuously flip this coin thousands of times in a row and record our results. While we can’t predict exactly which way the coin will land on any given toss, we can expect that, on average, the coin will land with the aforementioned 53/47 split.

Now because each coin toss constitutes an independent and identically distributed (IID) probability function, we can expect this sequence to obey certain properties. If as we are making our tosses, we are computing the “real-time” statistics of the percentage of head/tails results, and more specifically if we plot the spread (or difference) of those percentage results as we proceed we will see that the spread has very large swings as we first begin to toss our coin, but very quickly the variability in the spread becomes stable as more and more tosses (data) are available for us to average over. Mathematically, the boundary on these swings is inversely proportional to the square root of how many tosses are performed. In the “Moment of Truth” video on CVRs linked above, Jeff and Walter refer to this as a “Cone of Probability”, and he generates his boundary curves experimentally. He is correct. It is a cone of probability as its really just a manifestation of well-known and well-understood Poisson Noise characteristic (for the math nerds reading this). In Jeff’s work he uses the ratio of votes between candidates, while I’m using the spread (or deviation) of the vote percentages. Both metrics are valid, but using the deviation has an easy closed-form boundary curve that we don’t need to generate experimentally.

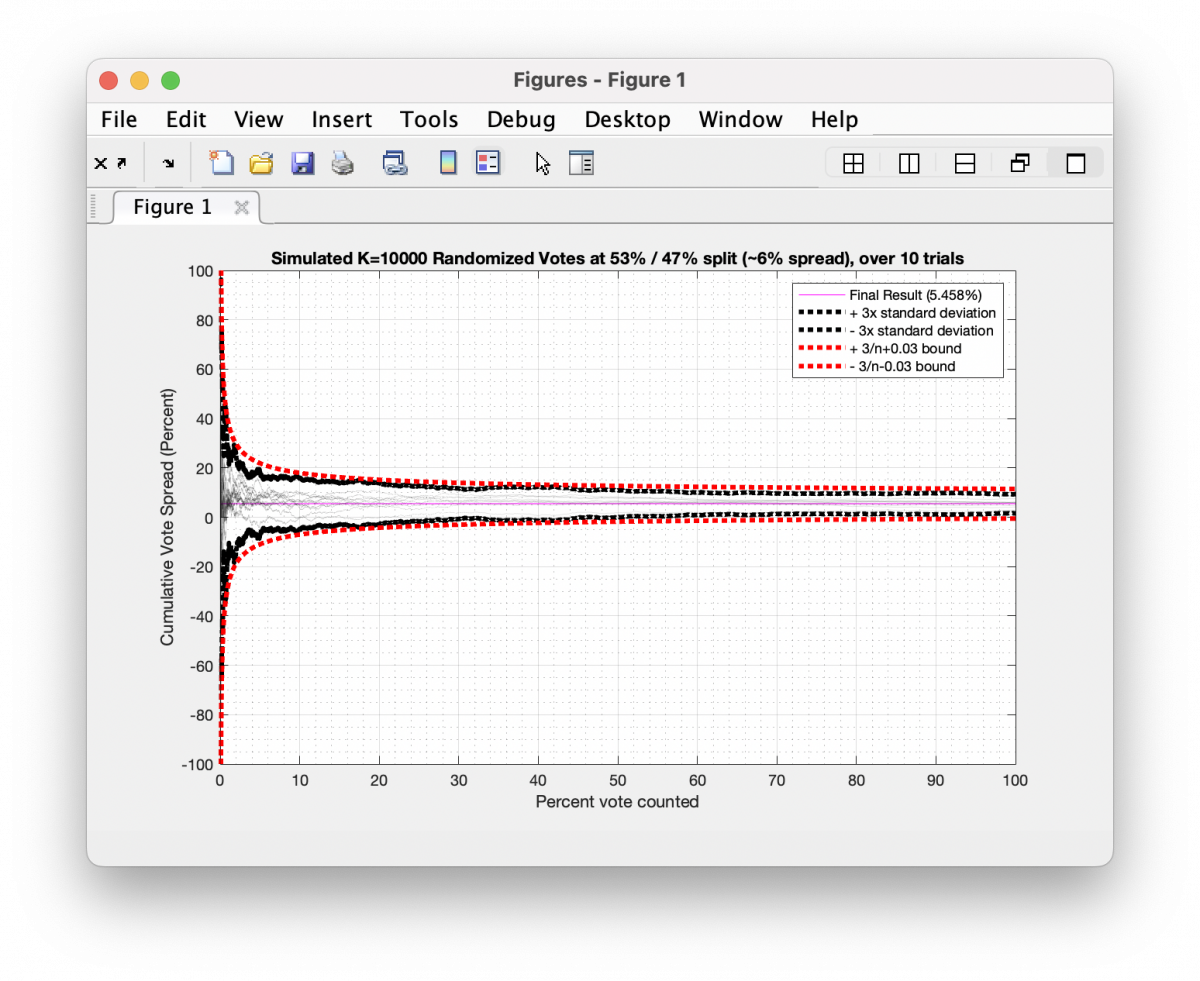
In the graphic below I have simulated 10 different trials of 10,000 tosses for a distribution that leans 53/47, which is equivalent to a 6% spread overall. Each trial had 10,000 random samples generated as either +1 or -1 values (a.k.a. a binary “Yes” or “No” vote) approximating the 53/47 split and I plotted the cumulative running spread of the results as each toss gets accumulated. The black dotted outline is the 95% confidence interval (or +/-3x the standard deviation) across the 10 trials for the Nth bin, and the red dotted outline is the 3/sqrt(n-1) analytical boundary.

So how does this apply to election data?

In a theoretically free and perfectly fair election we should see similar statistical behavior, where each coin toss is replaced with a ballot from an individual voter. In a perfect world we would have each vote be completely independent of every other vote in the sequence. In reality we have to deal with the fact that there can be small local regions of time in which perfectly legitimate correlations in the sequence of scanned ballots exist. Think of a local church who’s congregation is very uniform and they all go to the polls after Sunday mass. We would see a small trend in the data corresponding to this mass of similar thinking peoples going to the polls at the same time. But we wouldn’t expect there to be large, systematic patterns, or sharp discontinuities in the plotted results. A little bit of drift and variation is to be expected in dealing with real world election data, but persistent and distinct patterns would indicate a systemic issue.

Now we cannot isolate all of the variables in a real life example, but we should try as best as possible. To that effect, we should not mix different ballot types that are cast in different manners. We should keep our analysis focused within each sub-group of ballot type (mail-in, early-vote, day-of, etc). It is to the benefit of this analysis that the very nature of voting, and the procedures by which it occurs, is a very randomized process. Each sub-grouping has its own quasi-random process that we can consider.

While small groups (families, church groups) might travel to the in-person polls in correlated clusters, we would expect there to be fairly decent randomization of who shows up to in-person polls and when. The ordering of who stands in line before or after one another, how fast they check-in and fill out their ballot, etc, are all quasi-random processes.

Mail-in ballots have their own randomization as they depend on the timing of when individuals request, fill-out and mail their responses, as well as the logistics and mechanics of the postal service processes themselves providing a level of randomization as to the sequence of ballots being recorded. Like a dealer shuffling a deck of cards, the process of casting a mail-in vote provides an additional level of independence between samples.

No method is going to supply perfect theoretical independence from ballot to ballot in the sequence, but theres a general expectation that voting should at least be similar to an IID process.

Also … and I cannot stress this enough … while these techniques can supply indications of irregularities and discrepancies in elections data, they are not conclusive and must be coupled with in-depth investigations.

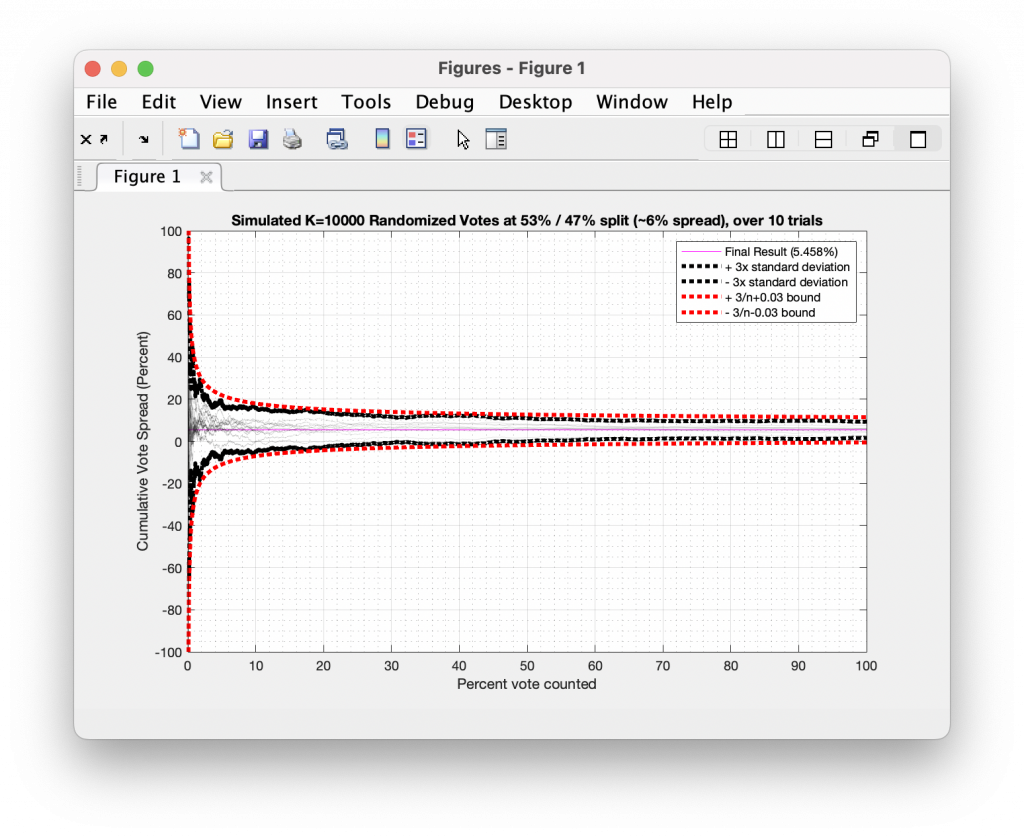
So going back to the simulation we generated above … what does a simulation look like when cheating occurs? Let’s take a very simple cheat from a random “elections” of 10,000 ballots, with votes being representative of either +1 (or “Yes”) or -1 (or “No”) as we did above. But lets also cheat by randomly selecting two different spots in the data stream to place blocks of 250 consecutive “Yes” results.

The image below shows the result of this process. The blue curve represents the true result, while the red curve represents the cheat. We see that at about 15% and 75% of the vote counted, our algorithm injected a block of “Yes” results, and the resulting cumulative curve breaks through the 3/sqrt(N-1) boundary. Now, not every instance or type of cheat will break through this boundary, and there may be real events that might explain such behavior. But looking for CVR curves that break our statistical expectations is a good way to flag items that need further investigation.

Computing the probability of a ballot run:

Section added on 2022-09-18

We can also a bit more rigor to the statistics outlier detection by computing the probability of the length of observed runs (e.g. how many “heads” did we get in a row?) occurring as we move through the sequential entries. We can compute this probability for K consecutive draws using the rules of statistical independence, which is P([a,a,a,a]) = P(a) x P(a) x P(a) x P(a) = P(a)^4. Therefore the probability of getting 4 “heads” in a row with a hypothetical 53/47 weighted coin would be .53^4 = 0.0789.

Starting with my updated analysis of 2021 Henrico County VA, I’ve started adding this computation to my plots. I have not yet re-run the Texas data below with this new addition, but will do so soon and update this page accordingly.

Real Examples

So I haven’t gotten complete cast vote records from VA yet (… which is a whole other set of issues …), but I have gotten my Cheeto stained fingers on some data from the Travis County Texas 2020 race.

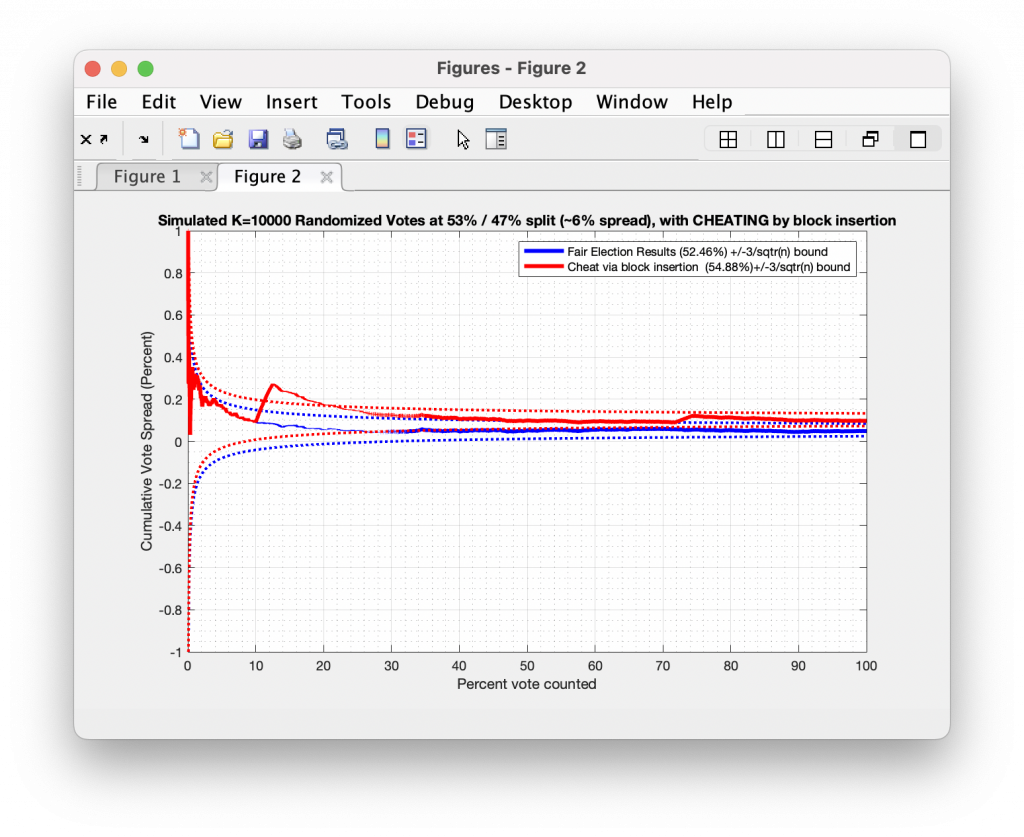
So let us first take a look at an example of a real race where everything seems to be obeying the rules as set out above. I’ve doubled my error bars from 3x to 6x of the inverse square standard (discussed above) in order to handle the quasi-IID nature of the data and give some extra margin for small fluctuating correlations.

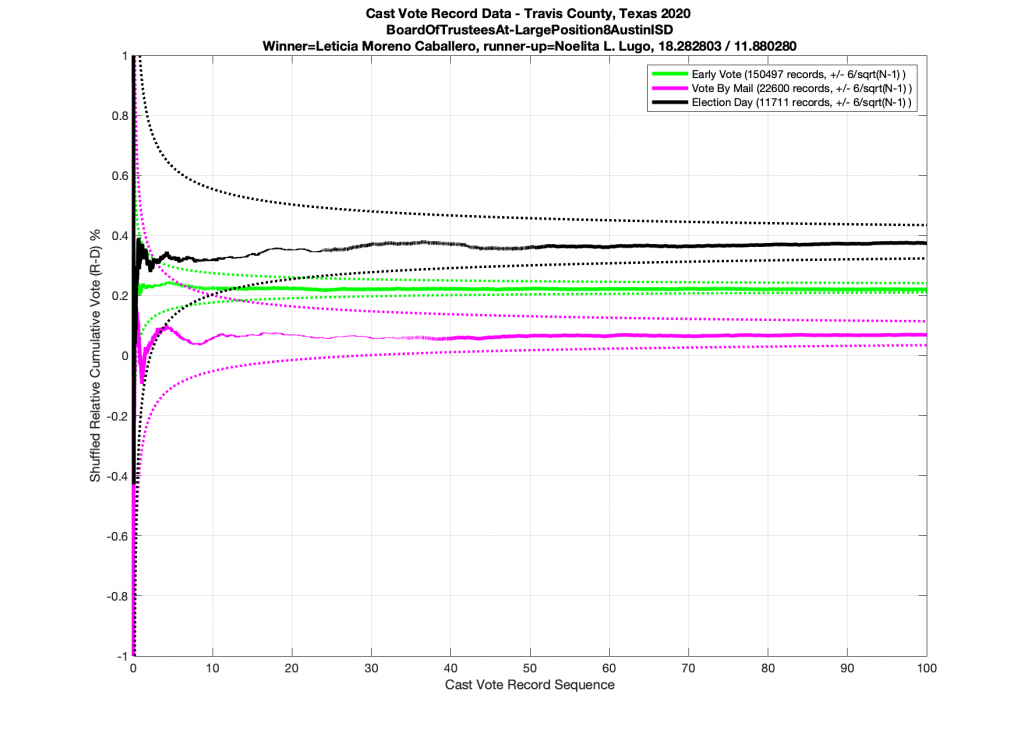
The plot below shows the Travis County Texas 2020 BoardOfTrusteesAt_LargePosition8AustinISD race, as processed by the tabulation system and stratified by ballot type. We can see that all three ballot types start off with large variances in the computed result but very quickly coalesce and approach their final values. This is exactly what we would expect to see.

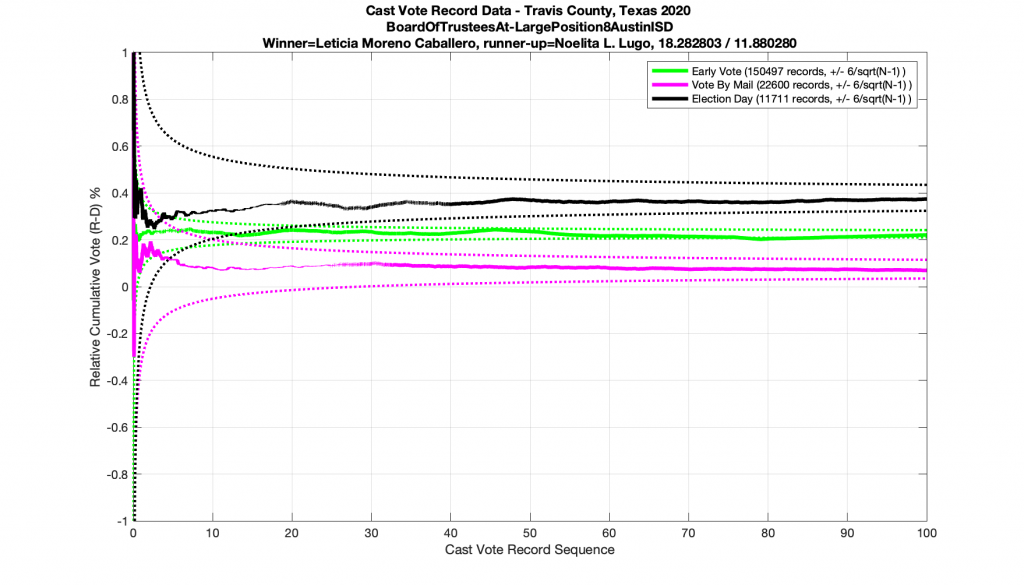
Now if I randomly shuffle the ordering of the ballots in this dataset and replot the results (below) I get a plot that looks unsurprisingly similar, which suggests that these election results were likely produced by a quasi-IID process.

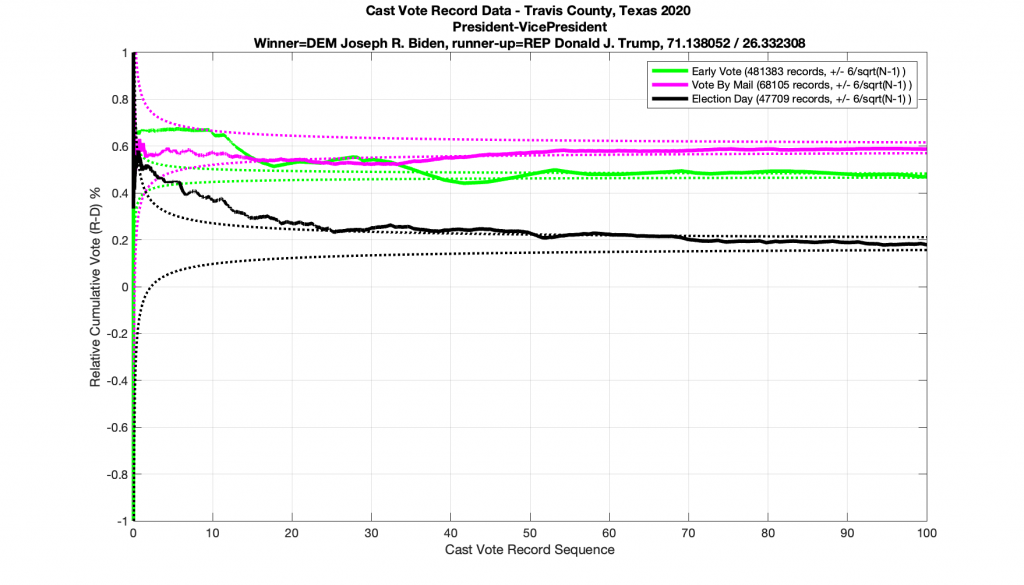
Next let’s take a look at a race that does NOT conform to the statistics we’ve laid out above. (… drum-roll please … as this the one everyone’s been waiting for). Immma just leave this right here and just simply point out that all 3 ballot type plots below in the Presidential race for 2020 go outside of the expected error bars. I also note the discrete stair step pattern in the early vote numbers. It’s entirely possible that there is a rational explanation for these deviations. I would sure like to hear it, especially since we have evidence from the exact same dataset of other races that completely followed the expected boundary conditions. So I don’t think this is an issue with a faulty dataset or other technical issues.

And just for completeness, when I artificially shuffle the data for the Presidential race, and force it to be randomized, I do in fact end up with results that conform to IID statistics (below).

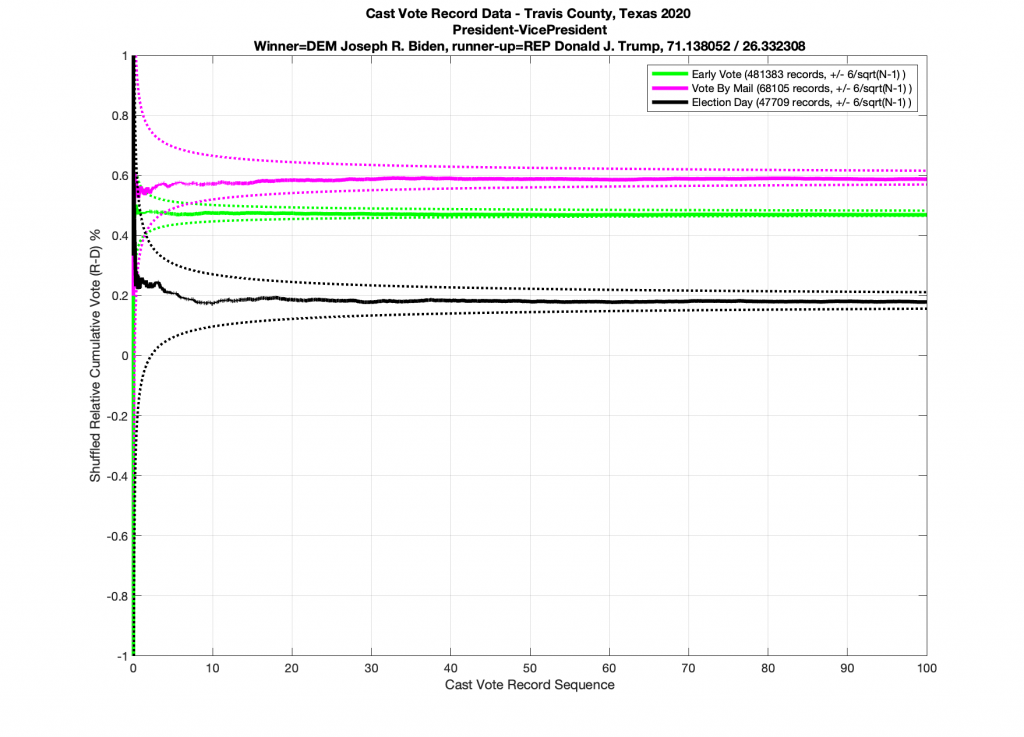
I will again state that while these results are highly indicative that there were irregularities and discrepancies in the election data, they are not conclusive. A further investigation must take place, and records must be preserved, in order to discover the cause of the anomalies shown.

Running through each race that had at least 1000 ballots cast and automatically detecting which races busted the 6/sqrt(n-1) boundaries produces the following tabulated results. A 1 in the right hand column indicates that the CVR data for that particular race in Travis County has crossed the error bounds. A 0 in the right hand column indicates that all data stayed within the error bound limits.

Race	CVR_OOB_Irregularity_Detected
President_VicePresident	1
UnitedStatesSenator	1
UnitedStatesRepresentativeDistrict10	1
UnitedStatesRepresentativeDistrict17	1
UnitedStatesRepresentativeDistrict21	1
UnitedStatesRepresentativeDistrict25	1
UnitedStatesRepresentativeDistrict35	0
RailroadCommissioner	1
ChiefJustice_SupremeCourt	1
Justice_SupremeCourt_Place6_UnexpiredTerm	1
Justice_SupremeCourt_Place7	1
Justice_SupremeCourt_Place8	1
Judge_CourtOfCriminalAppeals_Place3	1
Judge_CourtOfCriminalAppeals_Place4	1
Judge_CourtOfCriminalAppeals_Place9	1
Member_StateBoardOfEducation_District5	1
Member_StateBoardOfEducation_District10	1
StateSenator_District21	0
StateSenator_District24	1
StateRepresentativeDistrict47	1
StateRepresentativeDistrict48	1
StateRepresentativeDistrict49	1
StateRepresentativeDistrict50	1
StateRepresentativeDistrict51	0
ChiefJustice_3rdCourtOfAppealsDistrict	1
DistrictJudge_460thJudicialDistrict	1
DistrictAttorney_53rdJudicialDistrict	1
CountyJudge_UnexpiredTerm	1
Judge_CountyCourtAtLawNo_9	1
Sheriff	1
CountyTaxAssessor_Collector	1
CountyCommissionerPrecinct1	1
CountyCommissionerPrecinct3	1
AustinCityCouncilDistrict2	0
AustinCityCouncilDistrict4	0
AustinCityCouncilDistrict6	0
AustinCityCouncilDistrict7	0
AustinCityCouncilDistrict10	1
PropositionACityOfAustin_FP__2015_	1
PropositionBCityOfAustin_FP__2022_	1
MayorCityOfCedarPark	0
CouncilPlace2CityOfCedarPark	0
CouncilPlace4CityOfCedarPark	0
CouncilPlace6CityOfCedarPark	0
CouncilMemberPlace2CityOfLagoVista	0
CouncilMemberPlace4CityOfLagoVista	0
CouncilMemberPlace6CityOfLagoVista	0
CouncilMemberPlace2CityOfPflugerville	0
CouncilMemberPlace4CityOfPflugerville	0
CouncilMemberPlace6CityOfPflugerville	0
Prop_ACityOfPflugerville_2169_	0
Prop_BCityOfPflugerville_2176_	0
Prop_CCityOfPflugerville_2183_	0
BoardOfTrusteesDistrict2SingleMemberDistrictAISD	0
BoardOfTrusteesDistrict5SingleMemberDistrictAISD	0
BoardOfTrusteesAt_LargePosition8AustinISD	1
BoardOfTrusteesPlace1EanesISD	1
Prop_AEanesISD_2246_	0
BoardOfTrusteesPlace3LeanderISD	0
BoardOfTrusteesPlace4LeanderISD	0
BoardOfTrusteesPlace5ManorISD	1
BoardOfTrusteesPlace6ManorISD	0
BoardOfTrusteesPlace7ManorISD	1
BoardOfTrusteesPlace6PflugervilleISD	1
BoardOfTrusteesPlace7PflugervilleISD	1
BoardOfTrusteesPlace1RoundRockISD	1
BoardOfTrusteesPlace2RoundRockISD	0
BoardOfTrusteesPlace6RoundRockISD	0
BoardOfTrusteesPlace7RoundRockISD	0
BoardOfTrusteesWellsBranchCommunityLibraryDistrict	0
Var147	0
BoardOfTrusteesWestbankLibraryDistrict	0
Var150	0
Var151	0
DirectorsPlace2WellsBranchMUD	0
DirectorsPrecinct4BartonSprings_EdwardsAquiferConservationDistr	0
PropositionAExtensionOfBoundariesCityOfLakeway_1966_	0
PropositionB2_yearTermsCityOfLakeway_1973_	0
PropositionCLimitOnSuccessiveYearsOfServiceCityOfLakeway_1980_	0
PropositionDResidencyRequirementForCityManagerCityOfLakeway_198	0
PropositionEOfficeOfTreasurerCityOfLakeway_1994_	0
PropositionFOfficialBallotsCityOfLakeway_2001_	0
PropositionGAuthorizingBondsCityOfLakeway_2008_	0
PropositionALagoVistaISD_2253_	0
PropositionBLagoVistaISD_2260_	0
PropositionCLagoVistaISD_2267_	0
PropositionAEmergencyServicesDistrict1_2372_	0

References and further reading:

• [1] Forsberg, O.J. (2020). Understanding Elections through Statistics: Polling, Prediction, and Testing (1st ed.). Chapman and Hall/CRC. https://doi.org/10.1201/9781003019695
• [2] Klimek, Peter & Yegorov, Yuri & Hanel, Rudolf & Thurner, Stefan. (2012). Statistical Detection of Systematic Election Irregularities. Proceedings of the National Academy of Sciences of the United States of America. 109. 16469-73. https://doi.org/10.1073/pnas.1210722109.
• [3] https://www.amazon.com/dp/0367895374
• [4] https://www.researchgate.net/publication/238695138_Statistical_properties_of_electoral_systems_the_Mexican_case
• [5] https://en.wikipedia.org/wiki/Independent_and_identically_distributed_random_variables
• [6] https://radio.astro.gla.ac.uk/old_OA_course/pw/qf3.pdf
• [7] https://www.elections.virginia.gov/media/election-security/Virginia_Voting-System-Certification-Standard-FINAL.pdf
• [8] https://uscode.house.gov/view.xhtml?req=(title:52%20section:21081%20edition:prelim)
• [9] https://www.pnas.org/doi/10.1073/pnas.1210722109